如图作出 $f(x)$ 的图象，可知实数 $m$ 的取值范围是 $\left(0,\dfrac 14\right)$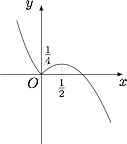． 此时 $x_1$ 是关于 $x$ 的方程\[2x^2-x=m\]的较小实根，$x_2,x_3$ 是关于 $x$ 的方程\[-x^2+x=m\]的两个实根．因此\[x_1=\dfrac{1-\sqrt{1+8m}}4,x_2x_3=m,\]因此问题转化为求函数\[y=\dfrac{1-\sqrt{1+8m}}4+m,m\in\left(0,\dfrac 14\right)\]的值域．令 $t=\sqrt{1+8m}$，则 $t$ 的取值范围是 $\left(1,\sqrt 3\right)$，此时\[y=\dfrac{1-t}4+\dfrac {t^2-1}8=\dfrac{(t-1)^2}{8},\]因此所求的取值范围是 $\left(0,\dfrac{2-\sqrt 3}4\right)$．
其他解法将 $x_1+x_2x_3$ 转化为关于 $x_1$ 的表达式，因为\[x_2x_3=m=2x_1^2-x_1,\]所以 $x_1+x_2x_3=x_1^2$，关键是求 $x_1$ 的取值范围．
因为 $x_1$ 是$$0<2x^2-x<\dfrac 14$$的小根，解得 $x_1\in\left(\dfrac{1-\sqrt 3}4,0\right)$，从而有$$x_1+x_2x_3\in\left(0,\dfrac{2-\sqrt 3}4\right).$$