点集 $M=\left\{(x,y)\mid x^2+y^2\leqslant 4x\leqslant 4\sqrt3y+8\leqslant 8+4\sqrt3\right\}$ 在平面直角坐标系 $xOy$ 内所对应的区域面积等于 ．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高二（二试）
【标注】
【答案】
$\dfrac{2\pi}{3}+\sqrt3$
【解析】
原题等价于下列不等式组所表示的可行域的面积$$\begin{cases} x^2+y^2\leqslant 4x,\\
x\leqslant \sqrt3y+2,\\
y\leqslant 1,\end{cases}$$如图．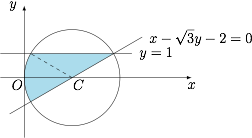
因此所求区域面积为 $\dfrac{2\pi}{3}+\sqrt3$．
x\leqslant \sqrt3y+2,\\
y\leqslant 1,\end{cases}$$如图．
因此所求区域面积为 $\dfrac{2\pi}{3}+\sqrt3$．
题目
答案
解析
备注
