设无穷项数列 $\{a_n\}$ 满足：$a_{n+1}a_n+3a_{n+1}+a_n+4=0$，若 $a_{2016}$ 为数列 $\{a_n\}$ 中的最小项，则 $a_1$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(-\dfrac{4031}{2015},-\dfrac{4033}{2016}\right)$
【解析】
考虑不动点方程为 $x^2+4x+4=0$，因此不动点为 $-2$，于是可以将数列递推公式改造为$$\dfrac{1}{a_{n+1}+2}-\dfrac{1}{a_n+2}=1.$$设 $f(x)=\dfrac{1}{x+2}$，则 $\{f(a_n)\}$ 成公差为 $1$ 的等差数列，如图．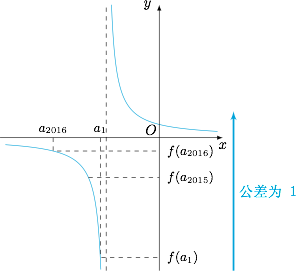
因此由 $f(a_{2016})=f(a_1)+2015\in (-1,0)$，可得$$-2016<\dfrac{1}{a_1+2}<-2015,$$解得 $a_1$ 的取值范围是 $\left(-\dfrac{4031}{2015},-\dfrac{4033}{2016}\right)$．
因此由 $f(a_{2016})=f(a_1)+2015\in (-1,0)$，可得$$-2016<\dfrac{1}{a_1+2}<-2015,$$解得 $a_1$ 的取值范围是 $\left(-\dfrac{4031}{2015},-\dfrac{4033}{2016}\right)$．
题目
答案
解析
备注
