数列 $\{a_n\}$ 满足:$a_{n-1}+a_{n+1}>2a_n(n>1,n\in \mathbb N^{\ast})$,给出下述命题:
① 若数列 $\{a_n\}$ 满足:$a_2>a_1$,则 $a_n>a_{n-1}(n>1,n\in \mathbb N^{\ast})$ 成立;
② 存在常数 $c$,使得 $a_n>c(n\in \mathbb N^{\ast})$ 成立;
③ 若 $p+q>m+n$(其中 $p,q,m,n\in\mathbb N^{\ast}$),则 $a_p+a_q>a_m+a_n$;
④ 存在常数 $d$,使得 $a_n>a_1+(n-1)d(n>1,n\in\mathbb N^{\ast})$ 都成立.
上述命题正确的是 .(写出所有正确结论的序号)
① 若数列 $\{a_n\}$ 满足:$a_2>a_1$,则 $a_n>a_{n-1}(n>1,n\in \mathbb N^{\ast})$ 成立;
② 存在常数 $c$,使得 $a_n>c(n\in \mathbb N^{\ast})$ 成立;
③ 若 $p+q>m+n$(其中 $p,q,m,n\in\mathbb N^{\ast}$),则 $a_p+a_q>a_m+a_n$;
④ 存在常数 $d$,使得 $a_n>a_1+(n-1)d(n>1,n\in\mathbb N^{\ast})$ 都成立.
上述命题正确的是
【难度】
【出处】
无
【标注】
【答案】
①④
【解析】
数列是一种特殊的函数,函数的性质很多都在数列中有体现,从函数的角度看数列,可以有效地利用我们已经熟悉的函数知识,比如各种初等函数及其性质,从而作出直观的判断或构造出反例.另一方面,数列是离散的,具有递推的性质,数列的性质问题,特别是单调性相关的问题有一个有力的武器——数列的差分:$$\Delta a_n=a_{n}-a_{n-1},$$(记 $a_0=0$).数列单调性的严格推导,往往需要考虑数列的差分.
从函数角度:本题关键条件 $a_{n-1}+a_{n+1}>2a_n(n>1,n\in \mathbb N^{\ast})$ 可以变形为$$\dfrac {a_{n-1}+a_{n+1}}2>a_n(n>1,n\in \mathbb N^{\ast})$$设 $a_n=f(n)$,则此条件表示 $(n-1,f(n-1))$ 和 $(n+1,f(n+1))$ 两点连线的中点高于点 $(n,f(n))$,如图: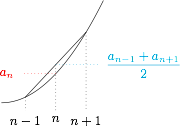 这反映了函数的凹凸性,满足这种性质的函数有三种情形:单增、单减、先减后增,如下图:
这反映了函数的凹凸性,满足这种性质的函数有三种情形:单增、单减、先减后增,如下图: 这三种情形中,单增的时候,数列增长越来越快;单减的时候,数列减少越来越慢;先减后增的时候,减少由快到慢,增长由慢到快.有了这样的直观理解,我们就可以借助这样的情况去对题中的几个命题尝试给出判断或构造反例.
这三种情形中,单增的时候,数列增长越来越快;单减的时候,数列减少越来越慢;先减后增的时候,减少由快到慢,增长由慢到快.有了这样的直观理解,我们就可以借助这样的情况去对题中的几个命题尝试给出判断或构造反例.
从数列的差分角度,题中关键条件$$a_{n-1}+a_{n+1}>2a_n(n>1,n\in \mathbb N^{\ast})$$即$$\Delta a_{n+1}>\Delta a_n.$$即数列 $\{a_n\}$ 的差分数列 $\{\Delta a_n\}$ 从第二项起单调递增,而 $\{a_n\}$ 是它的差分数列的前 $n$ 项和,即$$a_n=\sum_{i=1}^n{\Delta a_i}.$$于是,对于 ①,由 $a_2>a_1$ 知 $\Delta a_2>0$,而数列 $\{\Delta a_n\}$ 从第 $2$ 项起单调递增,所以 $n>1$ 时,$\Delta a_n\geqslant \Delta a_2>0$,① 正确.
对于 ②,由函数的性质知,当对应的函数单减且无下界时,② 错误,而底数小于 $1$ 的对数函数就满足,于是尝试构造 $a_n={\log_{\frac 12}}n$,从而知 ② 不正确.从数列差分角度,当一个数列单调递增时,它们的前 $n$ 项和数列可以没有下限,如取 $\Delta a_n=-\dfrac 1n$,则$$a_n=-\sum_{i=1}^n{\dfrac 1i},$$找不到常数 $c$,所以 ② 不正确.
对于 ③,数列 $\{a_n\}$ 可以单调递减,从而当 $p=q>m=n$ 时,显然不成立,用 ② 的反例即可.
对于 ④,因为$$a_n=a_1+\sum_{i=2}^n\Delta a_i\geqslant a_1+(n-1)\Delta a_2,$$故 ④ 成立.从函数角度来说,④ 的意思就是能够画出一条起点与 $(1,a_1)$ 重合,其它的点都在 $a_n=f(n)$ 下方的射线 $b_n=h(n)$ 来,事实上,三种情形都可以画出,如图: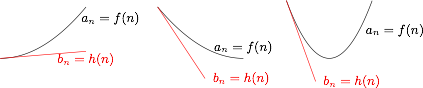 综上所述,命题正确的是 ①④.
综上所述,命题正确的是 ①④.
从函数角度:本题关键条件 $a_{n-1}+a_{n+1}>2a_n(n>1,n\in \mathbb N^{\ast})$ 可以变形为$$\dfrac {a_{n-1}+a_{n+1}}2>a_n(n>1,n\in \mathbb N^{\ast})$$设 $a_n=f(n)$,则此条件表示 $(n-1,f(n-1))$ 和 $(n+1,f(n+1))$ 两点连线的中点高于点 $(n,f(n))$,如图:
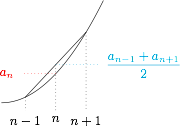 这反映了函数的凹凸性,满足这种性质的函数有三种情形:单增、单减、先减后增,如下图:
这反映了函数的凹凸性,满足这种性质的函数有三种情形:单增、单减、先减后增,如下图: 这三种情形中,单增的时候,数列增长越来越快;单减的时候,数列减少越来越慢;先减后增的时候,减少由快到慢,增长由慢到快.有了这样的直观理解,我们就可以借助这样的情况去对题中的几个命题尝试给出判断或构造反例.
这三种情形中,单增的时候,数列增长越来越快;单减的时候,数列减少越来越慢;先减后增的时候,减少由快到慢,增长由慢到快.有了这样的直观理解,我们就可以借助这样的情况去对题中的几个命题尝试给出判断或构造反例.从数列的差分角度,题中关键条件$$a_{n-1}+a_{n+1}>2a_n(n>1,n\in \mathbb N^{\ast})$$即$$\Delta a_{n+1}>\Delta a_n.$$即数列 $\{a_n\}$ 的差分数列 $\{\Delta a_n\}$ 从第二项起单调递增,而 $\{a_n\}$ 是它的差分数列的前 $n$ 项和,即$$a_n=\sum_{i=1}^n{\Delta a_i}.$$于是,对于 ①,由 $a_2>a_1$ 知 $\Delta a_2>0$,而数列 $\{\Delta a_n\}$ 从第 $2$ 项起单调递增,所以 $n>1$ 时,$\Delta a_n\geqslant \Delta a_2>0$,① 正确.
对于 ②,由函数的性质知,当对应的函数单减且无下界时,② 错误,而底数小于 $1$ 的对数函数就满足,于是尝试构造 $a_n={\log_{\frac 12}}n$,从而知 ② 不正确.从数列差分角度,当一个数列单调递增时,它们的前 $n$ 项和数列可以没有下限,如取 $\Delta a_n=-\dfrac 1n$,则$$a_n=-\sum_{i=1}^n{\dfrac 1i},$$找不到常数 $c$,所以 ② 不正确.
对于 ③,数列 $\{a_n\}$ 可以单调递减,从而当 $p=q>m=n$ 时,显然不成立,用 ② 的反例即可.
对于 ④,因为$$a_n=a_1+\sum_{i=2}^n\Delta a_i\geqslant a_1+(n-1)\Delta a_2,$$故 ④ 成立.从函数角度来说,④ 的意思就是能够画出一条起点与 $(1,a_1)$ 重合,其它的点都在 $a_n=f(n)$ 下方的射线 $b_n=h(n)$ 来,事实上,三种情形都可以画出,如图:
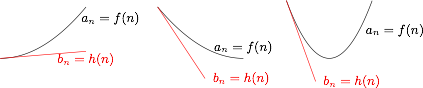 综上所述,命题正确的是 ①④.
综上所述,命题正确的是 ①④.
题目
答案
解析
备注