查看数据源：59ec77eec3f07000082a3d27
已知 $\triangle ABC$ 的外心为 $O$，$A$ 为定角且为锐角，$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$，$t$ 是正实数，则 $x+ty$ 的最大值是 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    向量
    >
    向量中的常用知识
    >
    三角形外心的向量表达
【答案】
$\dfrac{t+1-2\sqrt t\cos A}{2\sin^2A}$
【解析】
根据题意，有\[-\overrightarrow{OA}=x\left(\overrightarrow{OB}-\overrightarrow{OA}\right)+y\left(\overrightarrow{OC}-\overrightarrow{OA}\right),\]于是\[(x+y-1)\overrightarrow{OA}=x\overrightarrow{OB}+y\overrightarrow{OC},\]从而\[(x+y-1)^2=x^2+y^2+2xy\cos 2A,\]整理得\[2x+2y=4xy\sin^2A+1,\]同时，由于当 $A$ 为锐角时顶点 $A$ 在优弧 $BC$ 上，当 $A$ 为钝角时，顶点 $A$ 在劣弧 $BC$ 上，因此当 $A$ 为锐角时，有 $\dfrac{x}{x+y-1}$ 与 $\dfrac{y}{x+y-1}$ 不同时大于 $0$；当 $A$ 为钝角时，有 $\dfrac{x}{x+y-1}$ 与 $\dfrac{y}{x+y-1}$ 同时大于 $0$．当 $A$ 为锐角时，其可行域如图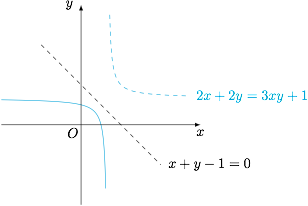．借助均值不等式可得有 $x+ty$（$t>0$）的最大值为\[\dfrac{t+1-2\sqrt t\cos A}{2\sin^2A}.\]
题目 答案 解析 备注
0.188007s