查看数据源：5a5b02951ccf88000838ad4b
在以 $O$ 为圆心，半径为 $10$ 的圆形区域内有相距为 $10$ 个两个垃圾处理厂 $A,B$，且 $AB$ 的中点为 $O$，若该区域内垃圾每公里运送 $A$ 处的费用是运送 $B$ 处的 $3$ 倍，则该区域内垃圾运往 $A$ 处的概率为 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的定义
    >
    阿波罗尼斯圆
  • 题型
    >
    计数与概率
    >
    概率计算题
  • 知识点
    >
    计数与概率
    >
    随机事件的概率
    >
    几何概型
【答案】
$\dfrac 9{64}$
【解析】
如图，设 $A(-5,0)$，$B(5,0)$，考虑到 $A$ 点距离与到 $B$ 点距离之比为 $\dfrac 13$ 的点 $P$ 的轨迹，根据阿波罗尼斯圆的定义，$P$ 点的轨迹是以 $M(-10,0)$，$N\left(-\dfrac 52,0\right)$ 为半径的圆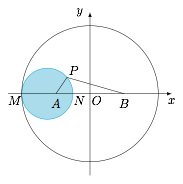．题中未加说明，我们认为该区域内每处发生需要运送的垃圾的可能相同，且会选择运费较低的方案．根据几何概型，该区域内的垃圾运往 $A$ 处的概率为\[\left(\dfrac{MN}{20}\right)^2=\dfrac 9{64}.\]
题目 答案 解析 备注
0.108167s