$x,y\in\mathbb R$,若 $|x|+|y|+|1-x|+|1-y|\leqslant 2$,则 $x+y$ 的取值范围是 .
【难度】
【出处】
2014年高考江西卷(文)
【标注】
【答案】
$[0,2]$
【解析】
我们熟知$$|x|+|1-x|\geqslant |x+(1-x)|=1,$$等号当且仅当 $0\leqslant x\leqslant 1$ 时取得,类似的,亦有$$|y|+|1-y|\geqslant |y+(1-y)|=1,$$等号当且仅当 $0\leqslant y\leqslant 1$ 时取得,于是题意即$$\begin{cases}0\leqslant x\leqslant 1,\\0\leqslant y\leqslant 1,\end{cases}$$该不等式组表示的可行域如图所示,于是 $x+y$ 的取值范围是 $[0,2]$.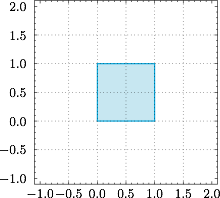

题目
答案
解析
备注