在区间 $\left[0,1\right]$ 上随机取两个数 $x$，$y$，记 $p_1$ 为事件“$x+y\geqslant \dfrac 12$”的概率，$p_2$ 为事件“${\left|{x-y}\right|}\leqslant \dfrac 12$”的概率，$p_3$ 为事件“$xy\leqslant \dfrac 12$”的概率，则 \((\qquad)\)
【难度】
【出处】
2015年高考湖北卷（理）
【标注】
【答案】
B
【解析】
本题属于几何概型中的“面积比”的模型．分别画出三个事件对应的图形，根据图形面积的大小估算概率的大小．$0\leqslant x \leqslant 1$，$0\leqslant y\leqslant 1$ 表示图中的正方形 $OACB$ 区域，事件 $p_1$ 中 $x+y\geqslant \dfrac 12$ 表示图中的阴影部分的区域，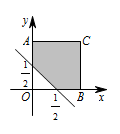
同理事件 $p_2$ 表示的区域如图：
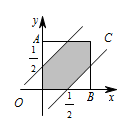事件 $p_3$ 表示的区域如图：
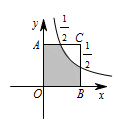对三者的面积进行比较，可得 $p_2<p_3<p_1$．
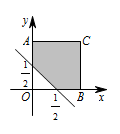同理事件 $p_2$ 表示的区域如图：事件 $p_3$ 表示的区域如图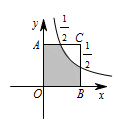：对三者的面积进行比较，可得 $p_2<p_3<p_1$．
题目
答案
解析
备注
