已知椭圆 $C:\dfrac{x^2}{4}+y^2=1$（$a>b>0$）的左顶点为 $A$，右顶点为 $B$，点 $P$ 是椭圆 $C$ 上位于 $x$ 轴上方的动点，直线 $AP$，$BP$ 与直线 $y=3$ 分别交于 $G,H$ 两点，则线段 $GH$ 的长度的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$8$
【解析】
考虑到 $\triangle PAB$ 与 $\triangle PGH$ 相似，所以过 $P$ 作 $x$ 轴的垂线，与 $AB,GH$ 分别交于点 $P_{1}$ 和点 $P_{2}$．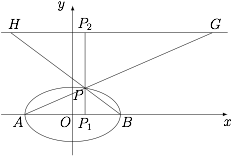
根据题意，设 $P$ 的纵坐标为 $p$，则有\[|GH|=\dfrac{|PP_{2}|}{|PP_{1}|}\cdot |AB|=\dfrac{3-p}{p}\cdot 4=4\left(\dfrac{3}{p}-1\right),\]根据椭圆的性质，$p$ 的最大值为 $1$，所以 $|GH|$ 的最小值为 $8$．
根据题意，设 $P$ 的纵坐标为 $p$，则有\[|GH|=\dfrac{|PP_{2}|}{|PP_{1}|}\cdot |AB|=\dfrac{3-p}{p}\cdot 4=4\left(\dfrac{3}{p}-1\right),\]根据椭圆的性质，$p$ 的最大值为 $1$，所以 $|GH|$ 的最小值为 $8$．
题目
答案
解析
备注
