已知函数 $f(x)=\dfrac{1+\ln x}{x-1}$，$g(x)=\dfrac kx$，其中 $k$ 是正整数．若对任意的 $c>1$，存在实数 $a,b$ 满足 $0<a<b<c$ 使得 $f(a)=g(b)=f(c)$，则 $k$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
先考虑 $f(x)$ 的导函数$$f'(x)=\dfrac{-\dfrac 1x-\ln x}{(x-1)^2}=\dfrac{\ln \dfrac 1x-\dfrac 1x}{(x-1)^2}<0,$$于是 $f(x)$ 在 $(0,1)$ 和 $(1,+\infty)$ 均单调递减，如图．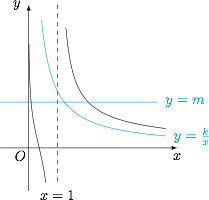
根据图象，可得问题等价于$$\begin{cases} f(x)<g(x),&x\in (0,1),\\ f(x)>g(x),&x \in (1,+\infty).\end{cases}$$取 $x=2$，可得$$k<2f(2)=2+2\ln 2,$$于是 $k\leqslant 3$．接下来验证 $k=3$ 符合题意．
（i）当 $x\in (0,1)$ 时，有$$f(x)<g(x)\Leftrightarrow \ln\dfrac 1x<\dfrac 3x-2,$$而$$\ln \dfrac 1x<\dfrac 1x-1<\dfrac 3x-2,$$不等式成立；
（ii）当 $x\in (1,+\infty)$ 时，有$$f(x)>g(x)\Leftrightarrow \ln x+\dfrac 3x-2>0.$$记右边为 $\varphi(x)$，那么其导函数$$\varphi'(x)=\dfrac{x-3}{x^2},$$因此 $\varphi(x)$ 的极小值，亦为最小值为 $\varphi(3)=\ln 3 -1>0$，不等式成立．
综上所述，所求 $k$ 的最大值为 $3$．
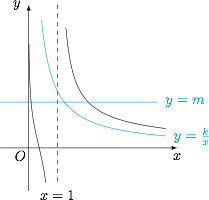根据图象，可得问题等价于$$\begin{cases} f(x)<g(x),&x\in (0,1),\\ f(x)>g(x),&x \in (1,+\infty).\end{cases}$$取 $x=2$，可得$$k<2f(2)=2+2\ln 2,$$于是 $k\leqslant 3$．接下来验证 $k=3$ 符合题意．（i）当 $x\in (0,1)$ 时，有$$f(x)<g(x)\Leftrightarrow \ln\dfrac 1x<\dfrac 3x-2,$$而$$\ln \dfrac 1x<\dfrac 1x-1<\dfrac 3x-2,$$不等式成立；
（ii）当 $x\in (1,+\infty)$ 时，有$$f(x)>g(x)\Leftrightarrow \ln x+\dfrac 3x-2>0.$$记右边为 $\varphi(x)$，那么其导函数$$\varphi'(x)=\dfrac{x-3}{x^2},$$因此 $\varphi(x)$ 的极小值，亦为最小值为 $\varphi(3)=\ln 3 -1>0$，不等式成立．
综上所述，所求 $k$ 的最大值为 $3$．
题目
答案
解析
备注
