设 $O$ 为 $\triangle ABC$ 的外心，$x \overrightarrow {OA}+y\overrightarrow {OB}+z\overrightarrow {OC}=\overrightarrow {0}$，$xyz\ne 0$，$C$ 为 $\triangle ABC$ 的内角，则 $\cos{2C}=$ ．（用 $x,y,z$ 表示）
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {z^2-x^2-y^2}{2xy}$
【解析】
由题意知当 $C$ 为锐角或直角时，有$$\langle \overrightarrow {OA},\overrightarrow {OB}\rangle=2C;$$当 $C$ 为钝角时，有$$\langle \overrightarrow {OA},\overrightarrow {OB}\rangle=2\pi-2C;$$记 $\langle \overrightarrow {OA},\overrightarrow {OB}\rangle=\theta$，则有 $\cos{2C}=\cos\theta$，不妨设 $\triangle ABC $ 的外接圆半径为 $1$，如图（在本题的条件下，$C$ 不可能为直角）：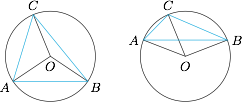
要得到 $\cos\theta$，我们将条件 $x \overrightarrow {OA}+y\overrightarrow {OB}+z\overrightarrow {OC}=\overrightarrow {0}$ 移项得：$$-z\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow {OB},$$将上式两边平方（即与自身作数量积）得$$z^2=x^2+y^2+2xy\cos\theta,$$从而有 $\cos2C=\cos\theta=\dfrac {z^2-x^2-y^2}{2xy}$．
要得到 $\cos\theta$，我们将条件 $x \overrightarrow {OA}+y\overrightarrow {OB}+z\overrightarrow {OC}=\overrightarrow {0}$ 移项得：$$-z\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow {OB},$$将上式两边平方（即与自身作数量积）得$$z^2=x^2+y^2+2xy\cos\theta,$$从而有 $\cos2C=\cos\theta=\dfrac {z^2-x^2-y^2}{2xy}$．
题目
答案
解析
备注
