关于 $x$ 的不等式 $(ax-1)(\ln x+ax)\geqslant 0$ 在 $(0,+\infty)$ 上恒成立,则实数 $a$ 的取值范围是 .
【难度】
【出处】
无
【标注】
【答案】
$\left(-\infty,-\dfrac{1}{\rm e}\right]\cup\left\{{\rm e}\right\}$
【解析】
根据题意,有\[\forall x>0,\left(a-\dfrac 1x\right)\left(a+\dfrac{\ln x}x\right)\geqslant 0,\]也即\[\forall x>0,a\leqslant \min\left\{\dfrac 1x,-\dfrac{\ln x}x\right\}\lor a\geqslant \max\left\{\dfrac 1x,-\dfrac{\ln x}x\right\}.\]考虑其反面,为\[\exists x>0,\min\left\{\dfrac 1x,-\dfrac{\ln x}x\right\}< a < \max\left\{\dfrac 1x,-\dfrac{\ln x}x\right\},\]用导数研究函数 $y=-\dfrac{\ln x}x$,并作出 $y=\dfrac 1x$ 与 $y=-\dfrac{\ln x}x$ 的图象如下: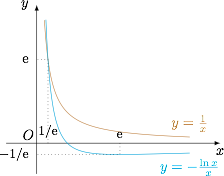 容易得到\[a>{\rm e}\lor -\dfrac{1}{\rm e}<a<{\rm e},\]于是所求的实数 $a$ 的取值范围是 $\left(-\infty,-\dfrac{1}{\rm e}\right]\cup\left\{{\rm e}\right\}$.
容易得到\[a>{\rm e}\lor -\dfrac{1}{\rm e}<a<{\rm e},\]于是所求的实数 $a$ 的取值范围是 $\left(-\infty,-\dfrac{1}{\rm e}\right]\cup\left\{{\rm e}\right\}$.
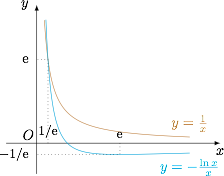 容易得到\[a>{\rm e}\lor -\dfrac{1}{\rm e}<a<{\rm e},\]于是所求的实数 $a$ 的取值范围是 $\left(-\infty,-\dfrac{1}{\rm e}\right]\cup\left\{{\rm e}\right\}$.
容易得到\[a>{\rm e}\lor -\dfrac{1}{\rm e}<a<{\rm e},\]于是所求的实数 $a$ 的取值范围是 $\left(-\infty,-\dfrac{1}{\rm e}\right]\cup\left\{{\rm e}\right\}$.
题目
答案
解析
备注