查看数据源：599165be2bfec200011df977
已知菱形 $ABCD$ 的边长为 $a$，$\angle ABC=60^\circ$，则 $\overrightarrow{BD}\cdot\overrightarrow{CD}=$  \((\qquad)\)
A: $-\dfrac 32a^2$
B: $-\dfrac 34a^2$
C: $\dfrac 34a^2$
D: $\dfrac 32a^2$
【难度】
【出处】
2015年高考山东卷（理）
【标注】
  • 知识点
    >
    向量
    >
    向量的运算
    >
    向量的数量积
  • 知识点
    >
    向量
    >
    向量的运算
    >
    向量的线性运算
  • 题型
    >
    向量
【答案】
D
【解析】
本小题属于有向线段的数量积问题，两个向量起点不同，故根据题中所给的夹角的关系，选择合适的起点与基底，使得 $\overrightarrow{BD}$ 与 $\overrightarrow {CD}$ 分别用基底表示，从而求得数量积．菱形 $ABCD$ 如图所示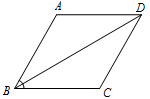：由平行四边形法则可得 $\overrightarrow{BD}=\overrightarrow {BA}+\overrightarrow{BC}$，所以\[\begin{split}\overrightarrow{BD}\cdot\overrightarrow{CD}&=\left(\overrightarrow {BA}+\overrightarrow{BC}\right)\cdot \overrightarrow{BA}\\&=\overrightarrow {BA}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot \overrightarrow{BA}\\&\overset{\left[a\right]}=\dfrac{3}{2}a^2\end{split}\]（推导中用到：[a]）
题目 答案 解析 备注
0.198981s