根据题意，函数 $f(x)$ 在区间 $[1,2)$ 上的最大值为\[f\left(\dfrac 32\right)=1,\]也即函数 $f(x)$ 在 $[1,2]$ 部分的图象是 $A_1(1,0)$，$B_1\left(\dfrac 32,1\right)$，$A_2(2,0)$ 形成的折线．又\[f(2x)=\dfrac 12f(x),\]于是定义\[A_k(2^{k-1},0),k=1,2,\cdots,\]以及\[B_k\left(\dfrac 32\cdot 2^{k-1},\dfrac{1}{2^{k-1}}\right),k=1,2,\cdots,\]则函数 $f(x)$ 的图象为折线 $A_1B_1A_2B_2\cdots A_nB_n\cdots$，如图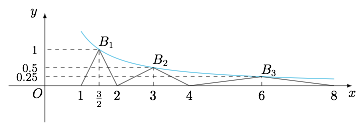．设函数 $g(x)=\dfrac 3{2x}$，则 $B_k$（$k=1,2,\cdots$）在函数 $g(x)$ 的图象上．注意到函数 $g(x)$ 在 $B_k$ 处的切线方程为\[y=-\dfrac 13\cdot 2^{3-2k} \left(x-\dfrac 32\cdot 2^{k-1}\right)+\dfrac{1}{2^{k-1}},\]而直线 $B_kA_{k+1}$ 的斜率为 $-2^{3-2k}$．因此函数 $g(x)$ 的图象除了 $B_k$（$k=1,2,\cdots$）外都在函数 $f(x)$ 的图象上方，而\[\dfrac 32\cdot 2^9=768<1000<\dfrac 32\cdot 2^{10},\]于是所求零点个数为 $10$．