不等式 $ \left|x-1 \right|- \left|x-5 \right|<2$ 的解集是 \((\qquad)\)
【难度】
【出处】
2015年高考山东卷（理）
【标注】
【答案】
A
【解析】
本小题考查解绝对值不等式问题．解绝对值不等式常用的方法有平方法，零点分段法和根据绝对值几何意义来解绝对值不等式，分析此题的形式可知，通过几何意义解绝对值不等式相对简便．由绝对值的几何意义可知，绝对值不等式 $ \left|x-1 \right|- \left|x-5 \right|<2$ 的解集是数轴上到 $1$ 的距离减去到 $5$ 的距离小于 $2$ 的点的集合．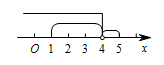
数轴上 $4$ 到 $1$ 的距离减去 $4$ 到 $5$ 的距离等于 $2$，所以不等式的解集为 $\left(-\infty,4\right)$．
数轴上 $4$ 到 $1$ 的距离减去 $4$ 到 $5$ 的距离等于 $2$，所以不等式的解集为 $\left(-\infty,4\right)$．
题目
答案
解析
备注
