过直线 $l:x+y=2$ 上任意点 $P$ 向圆 $C:x^2+y^2=1$ 作两条切线，切点分别为 $A,B$．线段 $AB$ 的中点为 $Q$，则点 $Q$ 到直线 $l$ 的距离的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac{\sqrt 2}2,\sqrt 2\right)$
【解析】
过点 $A,O$ 分别作 $QH,OD$ 垂直于 $l$，垂足为 $H,D$，如图，有$$\dfrac {QH}{OD}=\dfrac {PQ}{PO}.$$由直角三角形的射影定理知$$PQ\cdot PO=PB^2=PO^2-1,$$所以有$$QH=\sqrt 2\cdot\dfrac{PO^2-1}{PO^2}=\sqrt 2\left(1-\dfrac{1}{PO^2}\right).$$因为 $PO\in[\sqrt 2,+\infty)$，可以得到 $QH\in\left[\dfrac{\sqrt 2}{2},\sqrt 2\right)$．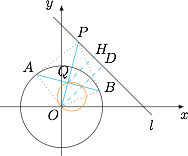
事实上，$Q$ 点的轨迹是直线 $l$ 对圆 $C$ 的反演圆：$$x\left(x-\dfrac 12\right)+y\left(y-\dfrac 12\right)=0.$$
事实上，$Q$ 点的轨迹是直线 $l$ 对圆 $C$ 的反演圆：$$x\left(x-\dfrac 12\right)+y\left(y-\dfrac 12\right)=0.$$
题目
答案
解析
备注
