已知 $x$，$y$ 满足约束条件 $\begin{cases}
x-y\geqslant 0,\\x+y\leqslant 2,\\y\geqslant 0.
\end{cases}$ 若 $z=ax+y$ 的最大值为 $4$，则 $a=$ \((\qquad)\)
x-y\geqslant 0,\\x+y\leqslant 2,\\y\geqslant 0.
\end{cases}$ 若 $z=ax+y$ 的最大值为 $4$，则 $a=$ \((\qquad)\)
【难度】
【出处】
2015年高考山东卷（理）
【标注】
【答案】
B
【解析】
此题主要考查含参线性规划问题．可以利用可行域是封闭图形，目标函数的最大值是在边界取得，故可以尝试将可行域的边界顶点带入，求出参数 $a$，但需要检验，此时是否取得最大值．题中不等式组所表示的可行域如图阴影部分所示：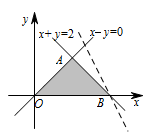
可行域是封闭图形，目标函数在 $O\left(0,0\right)$，$A\left(1,1\right)$，$B\left(2,0\right)$ 三点中的其中一点处能取到最大值．将 $O$ 点坐标带入目标函数 $y=-ax+z$，$z$ 不为 $4$；将 $A\left(1,1\right)$ 带入，解得 $a=3$，但当 $a=3$ 时，目标函数 $y=-3x+z$ 在 $B$ 处取得最大值；将 $B$ 点坐标带入目标函数，解得 $a=2$，此时目标函数 $y=-2x+z$ 在 $B$ 处取得最大值．综上，$a=2$．
可行域是封闭图形，目标函数在 $O\left(0,0\right)$，$A\left(1,1\right)$，$B\left(2,0\right)$ 三点中的其中一点处能取到最大值．将 $O$ 点坐标带入目标函数 $y=-ax+z$，$z$ 不为 $4$；将 $A\left(1,1\right)$ 带入，解得 $a=3$，但当 $a=3$ 时，目标函数 $y=-3x+z$ 在 $B$ 处取得最大值；将 $B$ 点坐标带入目标函数，解得 $a=2$，此时目标函数 $y=-2x+z$ 在 $B$ 处取得最大值．综上，$a=2$．
题目
答案
解析
备注
