查看数据源：599165be2bfec200011df97a
在梯形 $ABCD$ 中，$\angle ABC=\dfrac{\mathrm \pi} {2}$，$AD\parallel BC$，$BC=2AD=2AB=2$．将梯形 $ABCD$ 绕 $AD$ 所在的直线旋转一周而形成的曲面所围成的几何体的体积为 \((\qquad)\)
A: $\dfrac{2{\mathrm \pi} }{3}$
B: $\dfrac{4{\mathrm \pi} }{3}$
C: $\dfrac{5{\mathrm \pi} }{3}$
D: $2{\mathrm \pi} $
【难度】
【出处】
2015年高考山东卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
  • 题型
    >
    立体几何
【答案】
C
【解析】
此题属于求空间几何体的体积问题．此几何体是个旋转体，旋转后的几何体是个组合体，可以把其组合体分解成几个常见的几何体，求得体积．直角梯形 $ABCD$ 绕 $AD$ 旋转一周而形成的旋转体是由以线段 $AB$ 的长为底面圆半径，线段 $BC$ 为母线的圆柱挖去以线段 $CE$ 的长为底面圆半径，$ED$ 为高的圆锥剩余的几何体，如图所示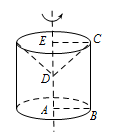：该几何体的体积为\[\begin{split}V&=V_{圆柱}-V_{圆锥}\\&={\mathrm \pi} \cdot AB^2\cdot BC-\dfrac{1}{3}\cdot {\mathrm \pi} \cdot CE^2\cdot DE\\&=\dfrac{5{\mathrm \pi} }{3} .\end{split}\]
题目 答案 解析 备注
0.128194s