查看数据源：599165c72bfec200011e13ed
正四棱锥的顶点都在同一球面上，若该棱锥的高为 $4$，底面边长为 $2$，则该球的表面积为 \((\qquad)\)
A: $\dfrac{{81{\mathrm \pi} }}{4}$
B: $16{\mathrm \pi} $
C: $9{\mathrm \pi} $
D: $\dfrac{{27{\mathrm \pi} }}{4}$
【难度】
【出处】
2014年高考大纲卷（文）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    多面体
    >
    棱锥
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的表面积
  • 题型
    >
    立体几何
【答案】
A
【解析】
正四棱锥的外接球的球心在此四棱锥的高（顶点与底面中心连线）上，将立体问题转化为平面问题，利用球心到各顶点的距离相等列出等量关系，从而解得球半径．即可解决此题．由正四棱锥的几何特征可知，正四棱锥的外接球的球心在其高上，设正四棱锥 $P-ABCD$ 的外接球的球心为 $O$，顶点 $P$ 在底面的射影为 $O_1$，如图所示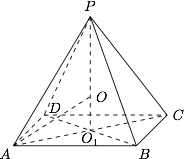．设 $OP=R$，则 $OA=R$，$OO_1=4-R$．因为底面边长为 $2$，所以 $O_1A=\sqrt 2$．在 $\mathrm {Rt}\triangle OAO_1$ 中，$OA^2=OO_1^2+O_1A^2$，故解得 $R=\dfrac{9}{4}$．因此外接球的表面积为 $S=4{\mathrm \pi} R^2=\dfrac{81{\mathrm \pi} }{4}$．
题目 答案 解析 备注
0.121702s