查看数据源：599165c72bfec200011e13ee
已知双曲线 $ C $ 的离心率为 $ 2 $，焦点为 ${F_1}$，${F_2}$，点 $ A $ 在 $ C $ 上，若 $\left| {{F_1}A} \right|= 2\left| {{F_2}A} \right|$，则 $\cos \angle A{F_2}{F_1} = $  \((\qquad)\)
A: $\dfrac{1}{4}$
B: $\dfrac{1}{3}$
C: $\dfrac{\sqrt 2 }{4}$
D: $\dfrac{\sqrt 2 }{3}$
【难度】
【出处】
2014年高考大纲卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    双曲线
    >
    双曲线的几何量
    >
    双曲线的基本量
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 知识点
    >
    解析几何
    >
    双曲线
    >
    双曲线的定义
    >
    双曲线的第一定义
  • 题型
    >
    解析几何
【答案】
A
【解析】
本题考查了双曲线的定义与余弦定理的应用．由双曲线的定义及题中的条件，可以用 $a$ 表示 $\triangle AF_1F_2$ 各边，进而用余弦定理解得 $\cos \angle AF_2F_1$．根据双曲线的定义有 $\left|F_1A\right|-\left|F_2A\right|=2a$，结合题中条件 $\left| {{F_1}A} \right|= 2\left| {{F_2}A} \right|$ 可得 $\left|F_1A\right|=4a$，$\left|F_2A\right|=2a$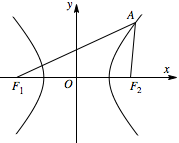．而 $\left|F_1F_2\right|=2c$，在 $\triangle AF_1F_2$ 中，由余弦定理得\[\cos \angle AF_2F_1=\dfrac {\left|AF_2\right|^2+\left|F_1F_2\right|^2-\left|AF_1\right|^2}{2\left|AF_2\right|\left|F_1F_2\right|}=\dfrac 14.\]
题目 答案 解析 备注
0.107843s