已知二面角 $\alpha - l - \beta $ 为 $60^\circ $,$AB \subset \alpha $,$AB \perp l$,$ A $ 为垂足,$CD \subset \beta $,$C \in l$,$\angle ACD = 135^\circ $,则异面直线 $AB$ 与 $CD$ 所成角的余弦值为 \((\qquad)\)
【难度】
【出处】
2014年高考大纲卷(理)
【标注】
【答案】
B
【解析】
求空间中直线的夹角时,可以用向量的方法,直接求其数量积,在计算过程中,为了计算方便,可设这两个向量的模长都为 $1$;也可以利用余弦定理,解得夹角,若是异面直线则需要先通过平移,构成三角形.不妨设 $\left|\overrightarrow {AB}\right|=\left|\overrightarrow {CD}\right|=1$,过点 $D$ 作 $DE\perp l$,交 $l$ 于点 $E$,如图: 故\[\begin{split}\overrightarrow {AB}\cdot\overrightarrow{CD}&=\overrightarrow{AB}\cdot\left(\overrightarrow{CE}+\overrightarrow{ED}\right)\\&=\overrightarrow {AB}\cdot \overrightarrow{ED}\\&=1\cdot \dfrac{\sqrt 2}{2}\cos 60^\circ \\&=\dfrac{\sqrt 2}{4},\end{split}\]故\[\cos\left \langle \overrightarrow {AB},\overrightarrow{CD}\right\rangle =\dfrac{\overrightarrow {AB}\cdot\overrightarrow {CD}}{\left|\overrightarrow {AB}\right|\cdot\left|\overrightarrow {CD}\right|}=\dfrac{\sqrt 2}{4} .\]如图,平移 $AB$ 到 $CE$,则异面直线 $AB$ 与 $CD$ 所成角即 $\angle ECD$.
故\[\begin{split}\overrightarrow {AB}\cdot\overrightarrow{CD}&=\overrightarrow{AB}\cdot\left(\overrightarrow{CE}+\overrightarrow{ED}\right)\\&=\overrightarrow {AB}\cdot \overrightarrow{ED}\\&=1\cdot \dfrac{\sqrt 2}{2}\cos 60^\circ \\&=\dfrac{\sqrt 2}{4},\end{split}\]故\[\cos\left \langle \overrightarrow {AB},\overrightarrow{CD}\right\rangle =\dfrac{\overrightarrow {AB}\cdot\overrightarrow {CD}}{\left|\overrightarrow {AB}\right|\cdot\left|\overrightarrow {CD}\right|}=\dfrac{\sqrt 2}{4} .\]如图,平移 $AB$ 到 $CE$,则异面直线 $AB$ 与 $CD$ 所成角即 $\angle ECD$.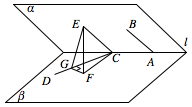 作 $CE$ 在 $\beta$ 上的投影 $CF$,则 $\angle ECF$ 即二面角 $\alpha - l - \beta $ 的平面角,由题意知\[\angle ECF=60^{\circ} .\]因为 $AB\perp l$,所以 $EC\perp l$,则根据三垂线定理可得 $CF\perp l$,所以\[\angle DCF=135^{\circ}-90^{\circ}=45^{\circ}.\]过点 $F$ 作 $FG\perp CD$ 于点 $G$,连接 $EG$,因为 $EF\perp \alpha$,所以 $EF\perp CD$,所以 $CD\perp 面 EFG$,所以 $CD\perp EG$.则在 $\mathrm {Rt}\triangle ECG$,$\mathrm {Rt}\triangle ECF$,$\mathrm {Rt}\triangle FCG$ 中分别有\[\cos \angle ECD=\dfrac {CG}{EC},\]\[\cos \angle ECF=\dfrac {CF}{EC},\]\[\cos \angle GCF=\dfrac {CF}{CG},\]由以上三式可得\[\cos \angle ECD=\cos \angle ECF\cos \angle FCG=\cos 60^{\circ}\cos 45^{\circ}=\dfrac {\sqrt 2}4.\]
作 $CE$ 在 $\beta$ 上的投影 $CF$,则 $\angle ECF$ 即二面角 $\alpha - l - \beta $ 的平面角,由题意知\[\angle ECF=60^{\circ} .\]因为 $AB\perp l$,所以 $EC\perp l$,则根据三垂线定理可得 $CF\perp l$,所以\[\angle DCF=135^{\circ}-90^{\circ}=45^{\circ}.\]过点 $F$ 作 $FG\perp CD$ 于点 $G$,连接 $EG$,因为 $EF\perp \alpha$,所以 $EF\perp CD$,所以 $CD\perp 面 EFG$,所以 $CD\perp EG$.则在 $\mathrm {Rt}\triangle ECG$,$\mathrm {Rt}\triangle ECF$,$\mathrm {Rt}\triangle FCG$ 中分别有\[\cos \angle ECD=\dfrac {CG}{EC},\]\[\cos \angle ECF=\dfrac {CF}{EC},\]\[\cos \angle GCF=\dfrac {CF}{CG},\]由以上三式可得\[\cos \angle ECD=\cos \angle ECF\cos \angle FCG=\cos 60^{\circ}\cos 45^{\circ}=\dfrac {\sqrt 2}4.\]
 故\[\begin{split}\overrightarrow {AB}\cdot\overrightarrow{CD}&=\overrightarrow{AB}\cdot\left(\overrightarrow{CE}+\overrightarrow{ED}\right)\\&=\overrightarrow {AB}\cdot \overrightarrow{ED}\\&=1\cdot \dfrac{\sqrt 2}{2}\cos 60^\circ \\&=\dfrac{\sqrt 2}{4},\end{split}\]故\[\cos\left \langle \overrightarrow {AB},\overrightarrow{CD}\right\rangle =\dfrac{\overrightarrow {AB}\cdot\overrightarrow {CD}}{\left|\overrightarrow {AB}\right|\cdot\left|\overrightarrow {CD}\right|}=\dfrac{\sqrt 2}{4} .\]如图,平移 $AB$ 到 $CE$,则异面直线 $AB$ 与 $CD$ 所成角即 $\angle ECD$.
故\[\begin{split}\overrightarrow {AB}\cdot\overrightarrow{CD}&=\overrightarrow{AB}\cdot\left(\overrightarrow{CE}+\overrightarrow{ED}\right)\\&=\overrightarrow {AB}\cdot \overrightarrow{ED}\\&=1\cdot \dfrac{\sqrt 2}{2}\cos 60^\circ \\&=\dfrac{\sqrt 2}{4},\end{split}\]故\[\cos\left \langle \overrightarrow {AB},\overrightarrow{CD}\right\rangle =\dfrac{\overrightarrow {AB}\cdot\overrightarrow {CD}}{\left|\overrightarrow {AB}\right|\cdot\left|\overrightarrow {CD}\right|}=\dfrac{\sqrt 2}{4} .\]如图,平移 $AB$ 到 $CE$,则异面直线 $AB$ 与 $CD$ 所成角即 $\angle ECD$. 作 $CE$ 在 $\beta$ 上的投影 $CF$,则 $\angle ECF$ 即二面角 $\alpha - l - \beta $ 的平面角,由题意知\[\angle ECF=60^{\circ} .\]因为 $AB\perp l$,所以 $EC\perp l$,则根据三垂线定理可得 $CF\perp l$,所以\[\angle DCF=135^{\circ}-90^{\circ}=45^{\circ}.\]过点 $F$ 作 $FG\perp CD$ 于点 $G$,连接 $EG$,因为 $EF\perp \alpha$,所以 $EF\perp CD$,所以 $CD\perp 面 EFG$,所以 $CD\perp EG$.则在 $\mathrm {Rt}\triangle ECG$,$\mathrm {Rt}\triangle ECF$,$\mathrm {Rt}\triangle FCG$ 中分别有\[\cos \angle ECD=\dfrac {CG}{EC},\]\[\cos \angle ECF=\dfrac {CF}{EC},\]\[\cos \angle GCF=\dfrac {CF}{CG},\]由以上三式可得\[\cos \angle ECD=\cos \angle ECF\cos \angle FCG=\cos 60^{\circ}\cos 45^{\circ}=\dfrac {\sqrt 2}4.\]
作 $CE$ 在 $\beta$ 上的投影 $CF$,则 $\angle ECF$ 即二面角 $\alpha - l - \beta $ 的平面角,由题意知\[\angle ECF=60^{\circ} .\]因为 $AB\perp l$,所以 $EC\perp l$,则根据三垂线定理可得 $CF\perp l$,所以\[\angle DCF=135^{\circ}-90^{\circ}=45^{\circ}.\]过点 $F$ 作 $FG\perp CD$ 于点 $G$,连接 $EG$,因为 $EF\perp \alpha$,所以 $EF\perp CD$,所以 $CD\perp 面 EFG$,所以 $CD\perp EG$.则在 $\mathrm {Rt}\triangle ECG$,$\mathrm {Rt}\triangle ECF$,$\mathrm {Rt}\triangle FCG$ 中分别有\[\cos \angle ECD=\dfrac {CG}{EC},\]\[\cos \angle ECF=\dfrac {CF}{EC},\]\[\cos \angle GCF=\dfrac {CF}{CG},\]由以上三式可得\[\cos \angle ECD=\cos \angle ECF\cos \angle FCG=\cos 60^{\circ}\cos 45^{\circ}=\dfrac {\sqrt 2}4.\]
题目
答案
解析
备注