若实数 $a,b$ 满足条件 $\begin{cases}
a+b-2\geqslant 0\\
b-a-1\leqslant 0\\
a\leqslant 1
\end{cases}$，则 $\dfrac{a+2b}{2a+b}$ 的最大值等于 ．
a+b-2\geqslant 0\\
b-a-1\leqslant 0\\
a\leqslant 1
\end{cases}$，则 $\dfrac{a+2b}{2a+b}$ 的最大值等于
【难度】
【出处】
2018年全国高中数学联赛吉林省预赛
【标注】
【答案】
$\dfrac{7}{5}$
【解析】
作出约束条件表示的可行域，如图，即 $\triangle ABC$ 内部和其边界，其中 $A(\dfrac{1}{2},\dfrac{3}{2}),B(1,1),C(1,2)$．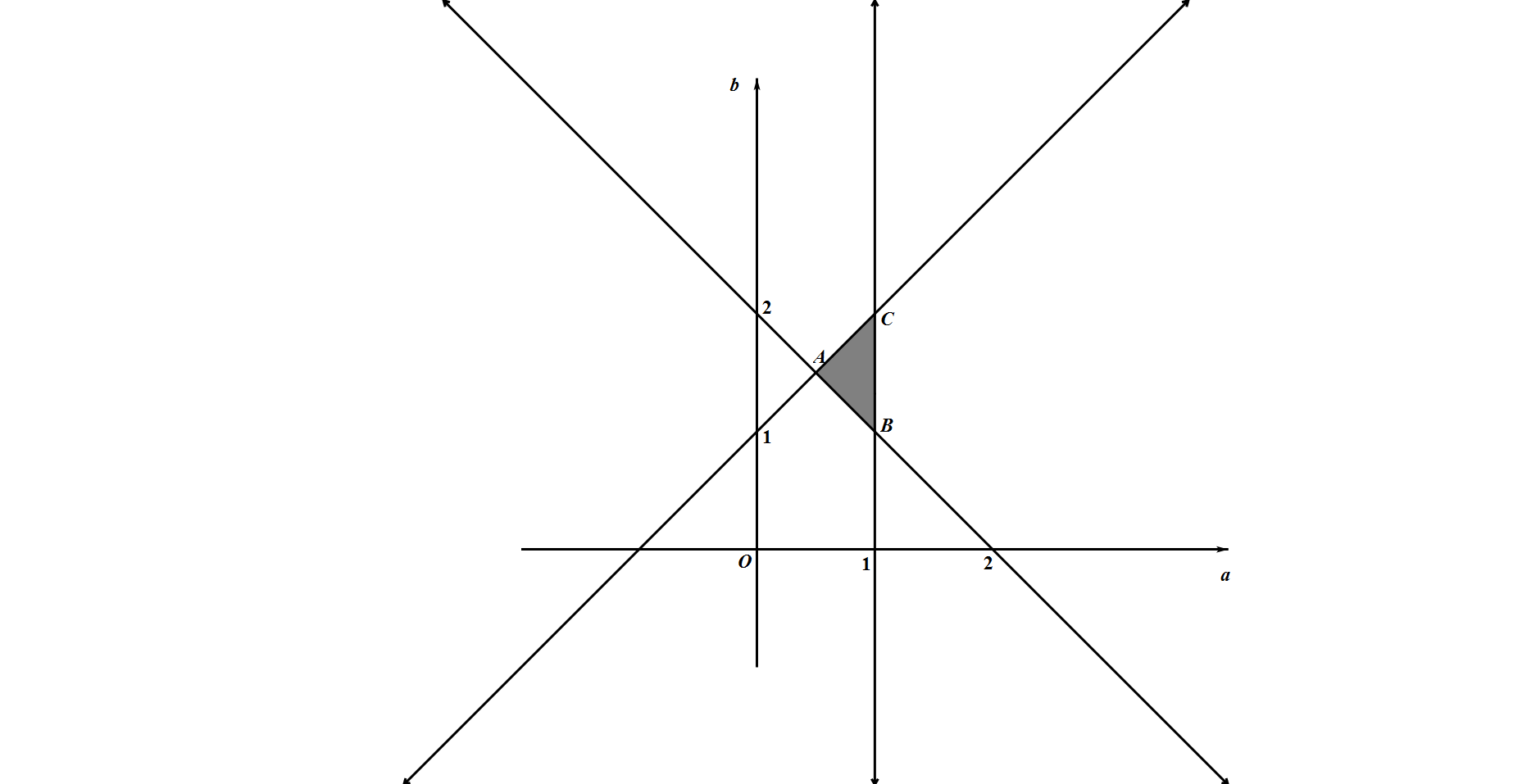
设 $P(a,b)$ 是可行域内任意一点，则 $k_{OP}=\dfrac{b}{a}$ 的最大值为 $k_{OA}=3$，最小值为 $k_{OB}=1$．故 $\dfrac{a+2b}{2a+b}=2-\dfrac{3a}{2a+b}=2-\dfrac{3}{2+\dfrac{b}{a}}$，可知当 $\dfrac{b}{a}$ 取最大值 $3$ 时，$\dfrac{a+2b}{2a+b}$ 也取得最大值为 $\dfrac{7}{5}$．
设 $P(a,b)$ 是可行域内任意一点，则 $k_{OP}=\dfrac{b}{a}$ 的最大值为 $k_{OA}=3$，最小值为 $k_{OB}=1$．故 $\dfrac{a+2b}{2a+b}=2-\dfrac{3a}{2a+b}=2-\dfrac{3}{2+\dfrac{b}{a}}$，可知当 $\dfrac{b}{a}$ 取最大值 $3$ 时，$\dfrac{a+2b}{2a+b}$ 也取得最大值为 $\dfrac{7}{5}$．
题目
答案
解析
备注
