如图,已知矩形 $ABCD$ 中,$AB=2AD,E$ 为边 $AB$ 的中点,将 $\triangle ADE$ 沿直线 $DE$ 翻折成 $A_1DE$.若 $M$ 为线段 $A_1C$ 的中点,则在 $\triangle ADE$ 翻折过程中,下列命题正确的是 .
(写出所有正确的命题编号)① 线段 $BM$ 的长是定值;② 存在某个位置,使 $DE\bot A_1C$;③ 点 $M$ 的运动轨迹是一个圆;④ 存在某个位置,使 $MB\bot$ 平面 $A_1DE$.
(写出所有正确的命题编号)① 线段 $BM$ 的长是定值;② 存在某个位置,使 $DE\bot A_1C$;③ 点 $M$ 的运动轨迹是一个圆;④ 存在某个位置,使 $MB\bot$ 平面 $A_1DE$.

【难度】
【出处】
2018年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
①③
【解析】
取 $CD$ 的中点 $F$,连结 $MF,BF$,则 $MF\parallel DA,BF\parallel DE$,所以平面 $MBF\parallel$ 平面 $A_1DE$,所以 $MB\parallel$ 平面 $A_1DE$.故 ③ 正确,④ 错误.由 $\angle A_1DE=\angle MFB,MF=\dfrac{1}{2}A_1D=$ 定值,$FB=DE=$ 定值,故由余弦定理可得 $MB^2=MF^2+FB^2-2MF\cdot FB\cdot \angle MFB$,所以 $MB$ 是定值,故 ① 正确.若 ② 成立,则由 $DE\bot CE$,可得 $DE\bot$ 面 $A_1EC$,所以 $DE\bot A_1E$,而这与 $DA_1\bot A_1E$ 矛盾,故 ② 错误.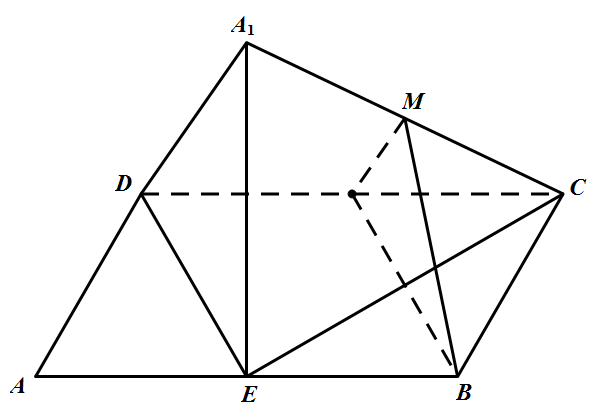

题目
答案
解析
备注