查看数据源：599165c62bfec200011e1111
一个多面体的三视图如图所示，则该多面体的表面积为 \((\qquad)\)
A: $21 + \sqrt 3 $
B: $18 + \sqrt 3 $
C: $ 21 $
D: $ 18 $
【难度】
【出处】
2014年高考安徽卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的表面积
  • 题型
    >
    立体几何
【答案】
A
【解析】
先由三视图还原几何体，再求表面积，其中还原是解题的关键，可联系正方体进行思考．根据三视图，知此多面体为如图所示正方体被面 $ABC$ 和面 $DEF$ 截掉两个三棱锥后剩下的几何体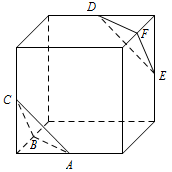．所以该多面体的表面积为\[ 6\cdot 2\cdot2- 6\cdot \dfrac 12\cdot 1\cdot1+2\cdot\dfrac 12 \cdot \sqrt 2\cdot \dfrac {\sqrt 6}{2}=21+\sqrt 3. \]
题目 答案 解析 备注
0.168053s