查看数据源：599165c62bfec200011e1049
如图，在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，点 $O$ 为线段 $BD$ 的中点．设点 $P$ 在线段 $C{C_1}$ 上，直线 $OP$ 与平面 ${A_1}BD$ 所成的角为 $\alpha $，则 $\sin \alpha $ 的取值范围是 \((\qquad)\)
A: $\left[\dfrac{\sqrt 3 }{3},1\right]$
B: $\left[\dfrac{\sqrt 6 }{3},1\right]$
C: $\left[\dfrac{\sqrt 6 }{3},\dfrac{2\sqrt 2 }{3}\right]$
D: $\left[\dfrac{2\sqrt 2 }{3},1\right]$
【难度】
【出处】
2014年高考四川卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    线面角
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 题型
    >
    立体几何
【答案】
B
【解析】
$OA_1$ 是 $OP$ 在面 $A_1DB$ 上的射影，直线 $OP$ 与平面 $A_1BD$ 所成的角为 $\angle A_1OP$ 或它的补角．利用余弦定理可解得“边界角”的余弦值．因为 $BD\perp 平面ACC_1A_1$，$BD\subset 平面A_1BD$，所以 $平面A_1BD\perp 平面ACC_1A_1$，所以 $OA_1$ 就是 $OP$ 在面 $A_1DB$ 上的射影，即直线 $OP$ 与平面 $A_1BD$ 所成的角为 $\angle A_1OP$ 或它的补角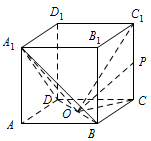．由于 $P$ 在线段 $CC_1$ 上运动，所以分析下 $P$ 运动到 $C$ 和 $C_1$ 的情况即可．
利用余弦定理，可求得 $\cos \angle A_1OC_1=\dfrac 13$，$\cos \angle A_1OC=-\dfrac {\sqrt 3}3$，所以 $\cos \angle A_1OP\in \left[-\dfrac {\sqrt 3}3,\dfrac 13 \right]$，所以 $\sin \alpha$ 的取值范围是 $\left[\dfrac {\sqrt 6}3,1\right]$．
题目 答案 解析 备注
0.110453s