查看数据源：599165c32bfec200011e076a
在平面直角坐标系中，$A$，$B $ 分别是 $x$ 轴和 $y$ 轴上的动点，若以 $AB$ 为直径的圆 $C$ 与直线 $2x+y-4=0$ 相切，则圆 $C$ 面积的最小值为 \((\qquad)\)
A: $\dfrac 4 5 {\mathrm{\mathrm \pi} }$
B: $\dfrac 3 4 {\mathrm{\mathrm \pi} }$
C: $\left(6-2 \sqrt 5\right) {\mathrm{\mathrm \pi} }$
D: $\dfrac 5 4 {\mathrm{\mathrm \pi} }$
【难度】
【出处】
2014年高考江西卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    直线
    >
    直线与直线的位置关系
    >
    点到直线的距离公式
  • 知识点
    >
    解析几何
    >
    直线与圆
    >
    直线与圆的位置关系
  • 知识点
    >
    解析几何
    >
    抛物线
    >
    抛物线的定义
  • 题型
    >
    解析几何
【答案】
A
【解析】
注意圆心 $C$ 的轨迹是抛物线，数形结合进行解决．如图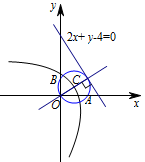，因为 $\angle AOB=90^\circ$，所以点 $O$ 在圆 $C$ 上，则点 $C$ 到点 $O$ 的距离等于它到直线 $2x+y-4=0$ 的距离，
故圆心 $C$ 的轨迹是以原点为焦点，以 $2x+y-4=0$ 为准线的抛物线．当圆心运动到图示位置时，圆 $C$ 的面积最小．
此时点 $O$ 到直线 $2x+y-4=0$ 的距离为\[\dfrac4{\sqrt{2^2+1^2}}=\dfrac4{\sqrt5},\]所以圆 $C$ 的最小半径为 $\dfrac2{\sqrt5}$，即圆 $C$ 面积的最小值为 $\dfrac 4 5 {\mathrm{\mathrm \pi} }$．
题目 答案 解析 备注
0.157737s