查看数据源：599165c22bfec200011e04f1
从正方形四个顶点及其中心这 $ 5 $ 个点中，任取 $ 2 $ 个点，则这 $ 2 $ 个点的距离不小于该正方形边长的概率为 \((\qquad)\)
A: $\dfrac{1}{5}$
B: $\dfrac{2}{5}$
C: $\dfrac{3}{5}$
D: $\dfrac{4}{5}$
【难度】
【出处】
2014年高考陕西卷（理）
【标注】
  • 知识点
    >
    计数与概率
    >
    随机事件的概率
    >
    古典概型
  • 题型
    >
    计数与概率
    >
    概率计算题
【答案】
C
【解析】
本题考查古典概型．从正方形四个顶点及其中心这 $ 5 $ 个点中，任取 $ 2 $ 个点，所有不同的取法有 $10$ 种，其中这 $ 2 $ 个点的距离不小于该正方形边长的取法有 $6$ 种，分别为 $AB,BC,CD,DA,AC,BD$．所以依古典概型概率计算公式得，所求概率为 $\dfrac 6{10}=\dfrac 35$．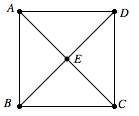
题目 答案 解析 备注
0.121761s