查看数据源：599165c22bfec200011e0420
已知函数 $f\left( x \right) = \begin{cases}
{x^2} + 1,&x > 0 ,\\
\cos x,&x \leqslant 0, \\
\end{cases}$ 则下列结论正确的是 \((\qquad)\)
A: $f\left( x \right)$ 是偶函数
B: $f\left( x \right)$ 是增函数
C: $f\left( x \right)$ 是周期函数
D: $f\left( x \right)$ 的值域为 $\left[ { - 1, + \infty } \right)$
【难度】
【出处】
2014年高考福建卷（理）
【标注】
  • 知识点
    >
    函数
    >
    分段函数
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    三角函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的奇偶性
    >
    载体
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的周期性
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
  • 题型
    >
    函数
【答案】
D
【解析】
根据基本初等函数的性质，画出函数图象即可．根据二次函数和余弦函数，画出分段函数 $f\left(x\right)$ 的图象如下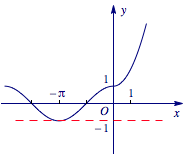．由图象知，函数 $f\left(x\right)$ 是非奇非偶函数，在定义域 $\mathbb R$ 内，不是单调递增函数，也不是周期函数，值域是 $\left[-1,+\infty\right)$．
题目 答案 解析 备注
0.184943s