设 $P,Q$ 分别为 ${x^2} + {\left( {y - 6} \right)^2} = 2$ 和椭圆 $\dfrac{x^2}{10} + {y^2} = 1$ 上的点，则 $P,Q$ 两点间的最大距离是 \((\qquad)\)
【难度】
【出处】
2014年高考福建卷（理）
【标注】
【答案】
D
【解析】
圆上的点与椭圆上的点的最大距离可以转化为圆心到椭圆的最大距离加上半径．如图所示，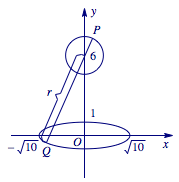
设以 $\left(0,6\right)$ 为圆心，以 $r$ 为半径的圆的方程为\[x^2+\left(y-6\right)^2=r^2\left(r>0\right),\]与椭圆方程$\dfrac{x^2}{10}+y^2=1$ 联立得方程组，消掉 $x^2$ 得\[9y^2+12y+r^2-46=0.\]令 $\Delta=12^2-4\cdot 9\left(r^2-46\right)=0$，解得 $r^2=50$，即 $r=5\sqrt2$．
由题意知，$P$，$Q$ 两点间的最大距离为 $r+\sqrt2=6\sqrt2$．
设以 $\left(0,6\right)$ 为圆心，以 $r$ 为半径的圆的方程为\[x^2+\left(y-6\right)^2=r^2\left(r>0\right),\]与椭圆方程$\dfrac{x^2}{10}+y^2=1$ 联立得方程组，消掉 $x^2$ 得\[9y^2+12y+r^2-46=0.\]令 $\Delta=12^2-4\cdot 9\left(r^2-46\right)=0$，解得 $r^2=50$，即 $r=5\sqrt2$．由题意知，$P$，$Q$ 两点间的最大距离为 $r+\sqrt2=6\sqrt2$．
题目
答案
解析
备注
