$a$，$b$ 为空间中两条互相垂直的直线，等腰直角三角形 $ABC$ 的直角边所在直线与 $a$，$b$ 都垂直，斜边 $AB$ 以直线 $AC$ 为旋转轴旋转，有下列结论：
$\text{ ① }$ 当直线 $AB$ 与 $a$ 成 $60^{\circ}$ 角时，$AB$ 与 $b$ 成 $30^{\circ}$ 角；
$\text{ ② }$ 当直线 $AB$ 与 $a$ 成 $60^{\circ}$ 角时，$AB$ 与 $b$ 成 $60^{\circ}$ 角；
$\text{ ③ }$ 直线 $AB$ 与 $a$ 所成角的最小值为 $45^{\circ}$；
$\text{ ④ }$ 直线 $AB$ 与 $a$ 所成角的最小值为 $60^{\circ}$．
其中正确的是 ．（填写所有正确结论的编号）
$\text{ ① }$ 当直线 $AB$ 与 $a$ 成 $60^{\circ}$ 角时，$AB$ 与 $b$ 成 $30^{\circ}$ 角；
$\text{ ② }$ 当直线 $AB$ 与 $a$ 成 $60^{\circ}$ 角时，$AB$ 与 $b$ 成 $60^{\circ}$ 角；
$\text{ ③ }$ 直线 $AB$ 与 $a$ 所成角的最小值为 $45^{\circ}$；
$\text{ ④ }$ 直线 $AB$ 与 $a$ 所成角的最小值为 $60^{\circ}$．
其中正确的是
【难度】
【出处】
2017年高考全国丙卷（理）
【标注】
【答案】
②③
【解析】
如图，设 $CD$ 为直线 $a$，$CE$ 为直线 $b$，过 $B$ 分别作 $a,b$ 的平行线 $BM,BN$，设 $\angle CBM=\theta$，直线 $AB$ 与直线 $a,b$ 所成的角分别为 $\alpha,\beta$．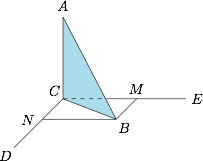
根据三射线定理，有\[\cos\alpha=\cos\angle ABM=\cos\angle CBA\cdot \cos\angle CBM=\dfrac{\sqrt 2}2\cdot \cos\theta,\]类似的，有\[\cos\beta=\cos\angle ABN=\cos\angle CBA\cdot \cos \angle CBN=\dfrac{\sqrt 2}2\cdot\sin\theta,\]据此易得命题 ②③ 正确．
注：直线 $AB$ 与直线 $a,b$ 所成的角分别为 $\alpha,\beta$，三射线定理部分也可以通过建系解决，令 $\overrightarrow{a}=(1,0,0),\overrightarrow{b}=(0,1,0)$，则可以取 $C(0,0,0),A(0,0,1)$，则点 $B$ 可以设为 $(\cos\theta,\sin\theta,0)$，于是 $\overrightarrow{AB}=(\cos\theta,\sin\theta,-1)$，从而有$$\overrightarrow{AB}\cdot\overrightarrow{a}=\cos \theta=\sqrt 2\cos\alpha,\overrightarrow{AB}\cdot\overrightarrow{b}=\sin\theta=\sqrt 2\cos\beta.$$以下同上．
根据三射线定理，有\[\cos\alpha=\cos\angle ABM=\cos\angle CBA\cdot \cos\angle CBM=\dfrac{\sqrt 2}2\cdot \cos\theta,\]类似的，有\[\cos\beta=\cos\angle ABN=\cos\angle CBA\cdot \cos \angle CBN=\dfrac{\sqrt 2}2\cdot\sin\theta,\]据此易得命题 ②③ 正确．注：直线 $AB$ 与直线 $a,b$ 所成的角分别为 $\alpha,\beta$，三射线定理部分也可以通过建系解决，令 $\overrightarrow{a}=(1,0,0),\overrightarrow{b}=(0,1,0)$，则可以取 $C(0,0,0),A(0,0,1)$，则点 $B$ 可以设为 $(\cos\theta,\sin\theta,0)$，于是 $\overrightarrow{AB}=(\cos\theta,\sin\theta,-1)$，从而有$$\overrightarrow{AB}\cdot\overrightarrow{a}=\cos \theta=\sqrt 2\cos\alpha,\overrightarrow{AB}\cdot\overrightarrow{b}=\sin\theta=\sqrt 2\cos\beta.$$以下同上．
题目
答案
解析
备注
