已知双曲线 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（$a>0$，$b>0$）的右顶点为 $A$，以 $A$ 为圆心，$b$ 为半径作圆 $A$，圆 $A$ 与双曲线 $C$ 的一条渐近线交于 $M$、$N$ 两点．若 $\angle{MAN}=60^{\circ}$，则 $C$ 的离心率为 ．
【难度】
【出处】
2017年高考全国乙卷（理）
【标注】
【答案】
$\dfrac{2\sqrt 3}{3}$
【解析】
如图所示：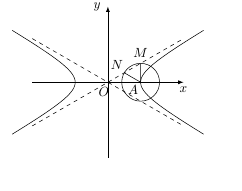
因为 $\angle{MAN}=60^{\circ}$，$MA=NA=b$，所以 $\triangle{MAN}$ 为等边三角形，所以 $A(a,0)$ 到渐近线 $bx-ay=0$ 的距离 $d=\dfrac{\sqrt 3}{2}b$，即$$d=\dfrac{ab}{\sqrt{a^2+b^2}}=\dfrac{ab}{c}=\dfrac{\sqrt 3}{2}b,$$所以$e=\dfrac ca=\dfrac 2{\sqrt 3}=\dfrac{2\sqrt 3}{3}$．
因为 $\angle{MAN}=60^{\circ}$，$MA=NA=b$，所以 $\triangle{MAN}$ 为等边三角形，所以 $A(a,0)$ 到渐近线 $bx-ay=0$ 的距离 $d=\dfrac{\sqrt 3}{2}b$，即$$d=\dfrac{ab}{\sqrt{a^2+b^2}}=\dfrac{ab}{c}=\dfrac{\sqrt 3}{2}b,$$所以$e=\dfrac ca=\dfrac 2{\sqrt 3}=\dfrac{2\sqrt 3}{3}$．
题目
答案
解析
备注
