已知 $\triangle ABC$，$AB=AC=4$，$BC=2$．点 $D$ 为 $AB$ 延长线上一点，$BD=2$，连结 $CD$，则 $\triangle BDC$ 的面积是 ，$\cos \angle BDC=$ ．
【难度】
【出处】
2017年高考浙江卷
【标注】
【答案】
$\dfrac {\sqrt {15}}{2}$；$\dfrac {\sqrt {10}}{4}$
【解析】
如图，分别取 $BC$、$DC$ 的中点 $E$、$F$，连结 $AE$、$BF$．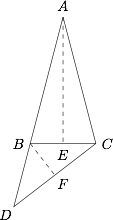
由题意，可得 $AE \perp BC$，$BF \perp DC$．在 $\triangle ABE$ 中，$\cos \angle ABC=\dfrac {BE}{AB}=\dfrac 14$，所以 $\cos \angle DBC=-\dfrac 14$，$\sin \angle DBC=\dfrac {\sqrt {15}}{4}$．所以$$S_{\triangle BCD}=\dfrac 12 BD\cdot BC \sin \angle DBC=\dfrac {\sqrt {15}}{2}.$$又因为$$\cos \angle DBC=1-2\sin^2 \angle DBF=-\dfrac 14,$$得 $\sin \angle DBF=\dfrac {\sqrt {10}}{4}$，所以 $\cos \angle BDC=\sin \angle DBF=\dfrac {\sqrt {10}}{4}$．
由题意，可得 $AE \perp BC$，$BF \perp DC$．在 $\triangle ABE$ 中，$\cos \angle ABC=\dfrac {BE}{AB}=\dfrac 14$，所以 $\cos \angle DBC=-\dfrac 14$，$\sin \angle DBC=\dfrac {\sqrt {15}}{4}$．所以$$S_{\triangle BCD}=\dfrac 12 BD\cdot BC \sin \angle DBC=\dfrac {\sqrt {15}}{2}.$$又因为$$\cos \angle DBC=1-2\sin^2 \angle DBF=-\dfrac 14,$$得 $\sin \angle DBF=\dfrac {\sqrt {10}}{4}$，所以 $\cos \angle BDC=\sin \angle DBF=\dfrac {\sqrt {10}}{4}$．
题目
答案
解析
备注
