已知 $a\in\mathbb R$,函数 $f(x)=\left|x+\dfrac 4x-a\right|+a$ 在区间 $[1,4]$ 上的最大值是 $5$,则 $a$ 的取值范围是 .
【难度】
【出处】
2017年高考浙江卷
【标注】
【答案】
$\left(-\infty,\dfrac 92\right]$
【解析】
考虑到\[f(x)=\left|g(x)-a\right|+a\]即\[f(x)=\begin{cases} 2a-g(x),& g(x)<a,\\ g(x),& g(x)\geqslant a,\end{cases}\]其几何意义为将函数 $g(x)$ 的图象在直线 $y=a$ 下方的部分翻折到直线 $y=a$ 上方.结合函数 $g(x)=x+\dfrac 4x$ 在 $[1,4]$ 上的图象,可得 $a$ 的取值范围是 $\left(-\infty,\dfrac 92\right]$.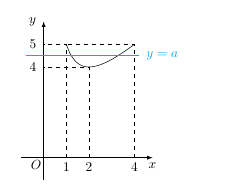

题目
答案
解析
备注