已知三棱锥的四个面都是腰长为 $2$ 的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是 ．
【难度】
【出处】
2016年高考四川卷（理）
【标注】
【答案】
$\dfrac{\sqrt3}{3}$
【解析】
本题考查由三棱锥的三视图求原图形的体积，根据三视图得到底面积和高是关键．因为三棱锥每个面都是腰为 $2$ 的等腰三角形，由正视图可得如下俯视图，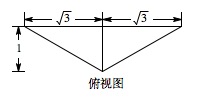
且三棱锥高为 $h=1$，则面积 $V=\dfrac{1}{3}Sh=\dfrac{1}{3}\cdot \left( \dfrac{1}{2}\cdot 2\sqrt{3}\cdot 1 \right)\cdot 1=\dfrac{\sqrt{3}}{3}$．
且三棱锥高为 $h=1$，则面积 $V=\dfrac{1}{3}Sh=\dfrac{1}{3}\cdot \left( \dfrac{1}{2}\cdot 2\sqrt{3}\cdot 1 \right)\cdot 1=\dfrac{\sqrt{3}}{3}$．
题目
答案
解析
备注
