查看数据源：599165c62bfec200011e10c5
已知 $m$，$n$ 表示两条不同直线，$\alpha $ 表示平面，下列说法正确的是 \((\qquad)\)
A: 若 $m\parallel \alpha$，$n\parallel \alpha $，则 $m\parallel n$
B: 若 $m \perp \alpha$，$n \subset \alpha $，则 $m \perp n$
C: 若 $m \perp \alpha $，$m \perp n$，则 $n\parallel \alpha $
D: 若 $m\parallel \alpha$，$m \perp n$，则 $n \perp \alpha $
【难度】
【出处】
2014年高考辽宁卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的平行关系
    >
    线面平行
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    点线面的位置关系
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    线面垂直
  • 题型
    >
    立体几何
【答案】
B
【解析】
可以拿正方体作为参照进行判断．若 $m \perp \alpha$，$n \subset \alpha $，则由线面垂直的概念可知 $m \perp n$，故 B 正确．接下来分析其他选项，如图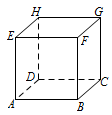：对于 A，$EF \parallel 面ABCD$，$ EH \parallel 面ABCD $，但 $EF\not \parallel EH $，所以 A 不正确；对于 C，$EA \perp 面ABCD$，$ EA \perp DA $，但 $DA\not \parallel 面 ABCD $，故 C 不正确；对于 D，$EF \parallel 面ABCD$，$ EF \perp EH $，但 $EH $ 不垂直面 $ABCD $，故 D 不正确．
题目 答案 解析 备注
0.108048s