曲线 $y=x^2$ 与直线 $y=x$ 所围成的封闭图形的面积为 ．
【难度】
【出处】
2015年高考天津卷（理）
【标注】
【答案】
$\dfrac 16$
【解析】
本题考查定积分的简单应用．如图：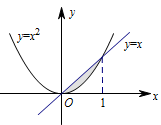
所求面积\[ \begin{split}S&\overset{\left[a\right]}=\int_0^1\left(x-x^2\right){\mathrm{d}}x\\&\overset{\left[b\right]}= \left. \left(\dfrac 12x^2-\dfrac 13x^3\right)\right |_0^1 \\&=\dfrac 16. \end{split}\]（推导中用到 $\left[a\right]$，$\left[b\right]$）
所求面积\[ \begin{split}S&\overset{\left[a\right]}=\int_0^1\left(x-x^2\right){\mathrm{d}}x\\&\overset{\left[b\right]}= \left. \left(\dfrac 12x^2-\dfrac 13x^3\right)\right |_0^1 \\&=\dfrac 16. \end{split}\]（推导中用到 $\left[a\right]$，$\left[b\right]$）
题目
答案
解析
备注
