设 $F$ 是双曲线 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 的一个焦点,若 $C$ 上存在点 $P$,使线段 $PF$ 的中点恰为其虚轴的一个端点,则 $C$ 的离心率为 .
【难度】
【出处】
2015年高考湖南卷(理)
【标注】
【答案】
$\sqrt 5$
【解析】
将点 $P$ 和点 $F$ 的中点代入渐近线方程,得到关于 $a,b,c$ 的等式,问题得到解决.设点 $F$ 为双曲线的右焦点,坐标为 $\left(c,0\right)$,根据中点坐标公式,得 $P\left(-c,2b\right)$,将其代入双曲线方程,得\[\dfrac{c^2}{a^2}-\dfrac{4b^2}{b^2}=1,\]解得双曲线的离心率$e=\dfrac{c}{a}=\sqrt5$.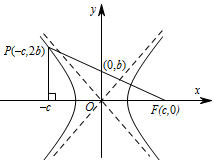

题目
答案
解析
备注