查看数据源：599165bf2bfec200011dfafc
函数 $f\left(x\right)=4{\cos^2}\dfrac x2 \cos\left(\dfrac{\mathrm \pi} 2-x\right)-2\sin x-{\left|{\ln\left(x+1\right)}\right|}$ 的零点个数为 ．
【难度】
【出处】
2015年高考湖北卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    对数函数
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    三角函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 题型
    >
    函数
【答案】
$2$
【解析】
先对函数 $y=4{\cos^2}\dfrac x2 \cos\left(\dfrac{\mathrm \pi} 2-x\right)-2\sin x$ 进行整理，变成正弦型函数的形式，然后考虑与函数 $y=\left|\ln\left(x+1\right)\right|$ 的图象的交点个数．因为\[\begin{split}f\left(x\right)&\overset{\left[a\right]}=4{\cos^2}\dfrac x2 \sin x-2\sin x-{\left|{\ln\left(x+1\right)}\right|}\\&\overset{\left[b\right]}=\dfrac{4\left(1+\cos x\right)}2\cdot \sin x-2\sin x-{\left|{\ln\left(x+1\right)}\right|}\\&=2\sin x\cos x-{\left|{\ln\left(x+1\right)}\right|}\\&\overset{\left[c\right]}=\sin 2x-{\left|{\ln\left(x+1\right)}\right|}.\end{split}\]（推导中用到：[a][b][c]）则问题转化为 $ y=\sin 2x $与 $ y=|\ln\left(x+1\right)| $图象交点个数的问题，在同一直角坐标系下画出两个函数的图象，如图所示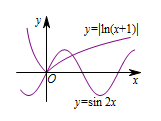：两个函数的图象有两个交点，所以函数 $f\left(x\right)=4{\cos^2}\dfrac x2 \cos\left(\dfrac{\mathrm \pi} 2-x\right)-2\sin x-{\left|{\ln\left(x+1\right)}\right|}$ 有两个零点．
题目 答案 解析 备注
0.124888s