如图，在三棱锥 $A-BCD$ 中，$AB=AC=BD=CD=3$，$AD=BC=2$，点 $M$，$N$ 分别为 $AD$，$BC$ 的中点，则异面直线 $AN$，$CM$ 所成的角的余弦值是 ．
【难度】
【出处】
2015年高考浙江卷（理）
【标注】
【答案】
$\dfrac 78$
【解析】
本题的重点在于找点作平行线，构造出异面直线所成角．如图，连接 $ DN $，取 $ DN $ 的中点为 $ K $，连接 $ MK $、$CK $．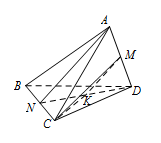
则 $ \angle CMK$ 为异面直线 $AN$，$CM$ 所成的角．
在 $ \triangle CMK $ 中，$MK=\sqrt 2$，$CM=2\sqrt 2$，$CK=\sqrt 3$，利用余弦定理可得 $\cos CMK=\dfrac 78$．
则 $ \angle CMK$ 为异面直线 $AN$，$CM$ 所成的角．在 $ \triangle CMK $ 中，$MK=\sqrt 2$，$CM=2\sqrt 2$，$CK=\sqrt 3$，利用余弦定理可得 $\cos CMK=\dfrac 78$．
题目
答案
解析
备注
