设常数 $a$ 使方程 $\sin x + \sqrt 3 \cos x = a$ 在闭区间 $\left[ {0,2{\mathrm \pi} } \right]$ 上恰有三个解 ${x_1}$,${x_2}$,${x_3}$,则 ${x_1} + {x_2} + {x_3} = $ .
【难度】
【出处】
2014年高考上海卷(理)
【标注】
【答案】
$\dfrac{{7{\mathrm \pi} }}{3}$
【解析】
设 $y=\sin x + \sqrt 3 \cos x=2\sin\left(x+\dfrac {\mathrm \pi} {3}\right) $.
$\because$ 常数 $a$ 使方程 $\sin x + \sqrt 3 \cos x = a$ 在闭区间 $\left[ {0,2{\mathrm \pi} } \right]$ 上恰有三个解,
$\therefore 2\sin\left(x+\dfrac {\mathrm \pi} {3}\right)=\sqrt 3 $ 在闭区间 $\left[ {0,2{\mathrm \pi} } \right]$ 上有 $ 3 $ 个不同的 $ x $ 值.
$\therefore a=\sqrt 3 $.
如图,易知 ${x_1}=0$,${x_2}=\dfrac {\mathrm \pi} {3}$,${x_3}=2{\mathrm \pi} $.
$\therefore$ ${x_1} + {x_2} + {x_3} =\dfrac{{7{\mathrm \pi} }}{3} $.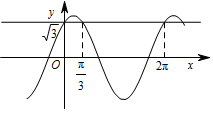
$\because$ 常数 $a$ 使方程 $\sin x + \sqrt 3 \cos x = a$ 在闭区间 $\left[ {0,2{\mathrm \pi} } \right]$ 上恰有三个解,
$\therefore 2\sin\left(x+\dfrac {\mathrm \pi} {3}\right)=\sqrt 3 $ 在闭区间 $\left[ {0,2{\mathrm \pi} } \right]$ 上有 $ 3 $ 个不同的 $ x $ 值.
$\therefore a=\sqrt 3 $.
如图,易知 ${x_1}=0$,${x_2}=\dfrac {\mathrm \pi} {3}$,${x_3}=2{\mathrm \pi} $.
$\therefore$ ${x_1} + {x_2} + {x_3} =\dfrac{{7{\mathrm \pi} }}{3} $.

题目
答案
解析
备注