已知 $f\left(x\right)$ 是定义在 $ {\mathbb{R}} $ 上且周期为 $3$ 的函数,当 $x \in \left[0,3\right)$ 时,$f\left(x\right) = \left|{x^2} - 2x + \dfrac{1}{2} \right|$.若函数 $y = f\left(x\right) - a$ 在区间 $\left[ - 3,4\right]$ 上有 $10$ 个零点(互不相同),则实数 $a$ 的取值范围是 .
【难度】
【出处】
2014年高考江苏卷
【标注】
【答案】
$\left(0,\dfrac{1}{2}\right)$
【解析】
画出 $f(x)$ 在区间 $[-3,4]$ 上的图象,上下平移直线 $y=a$,使它和函数 $y=f(x)$ 有 $10$ 个交点,即可得到 $a$ 的范围.根据图象变换和函数的周期性画出函数 $f\left(x\right)$ 的图象,根据题意 $f\left(x\right)$ 的图象和 直线 $y=a$ 在 $\left[-3,4\right]$ 上有 $10$ 个交点,所以实数 $a$ 的取值范围是 $\left(0,\dfrac{1}{2}\right)$.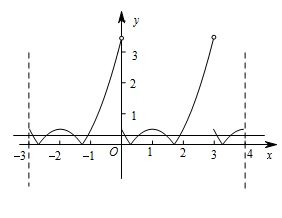

题目
答案
解析
备注