过圆外一点 $P$ 作圆的切线 $PA$（$A$ 为切点），再作割线 $PBC$ 依次交圆于 $B,C$，若 $PA = 6$，$AC = 8$，$BC = 9$，则 $AB = $ ．
【难度】
【出处】
2014年高考重庆卷（理）
【标注】
【答案】
$ 4 $
【解析】
可先利用圆幂定理求出 $PB$，然后利用相似求 $AB$．由切割线定理，得 $P{A^2} = PB \cdot PC = PB \cdot \left( {PB + BC} \right)$，解得 $ PB=3$．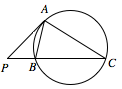
由弦切角定理，得 $\angle PAB=\angle PCA$，又 $\angle APB=\angle CPA $，则 $ \triangle APB\backsim \triangle CPA$，从而\[\dfrac{AB}{CA} = \dfrac{AP}{CP},\]即 $\dfrac{AB}{8} = \dfrac{6}{3 + 9}$，解得 $AB=4 $．
由弦切角定理，得 $\angle PAB=\angle PCA$，又 $\angle APB=\angle CPA $，则 $ \triangle APB\backsim \triangle CPA$，从而\[\dfrac{AB}{CA} = \dfrac{AP}{CP},\]即 $\dfrac{AB}{8} = \dfrac{6}{3 + 9}$，解得 $AB=4 $．
题目
答案
解析
备注
