由不等式组 $\begin{cases}
x \leqslant 0, \\
y \geqslant 0 ,\\
y - x - 2 \leqslant 0 \\
\end{cases}$ 确定的平面区域记为 ${\Omega _1}$，不等式组 $\begin{cases}x + y \leqslant 1, \\
x + y \geqslant - 2 \\
\end{cases}$ 确定的平面区域记为 ${\Omega _2}$，在 ${\Omega _1}$ 中随机取一点，则该点恰好在 ${\Omega _2}$ 内的概率为 \((\qquad)\)
x \leqslant 0, \\
y \geqslant 0 ,\\
y - x - 2 \leqslant 0 \\
\end{cases}$ 确定的平面区域记为 ${\Omega _1}$，不等式组 $\begin{cases}x + y \leqslant 1, \\
x + y \geqslant - 2 \\
\end{cases}$ 确定的平面区域记为 ${\Omega _2}$，在 ${\Omega _1}$ 中随机取一点，则该点恰好在 ${\Omega _2}$ 内的概率为 \((\qquad)\)
【难度】
【出处】
2014年高考湖北卷（理）
【标注】
【答案】
D
【解析】
作出平面区域，计算面积比即可．画出两部分图象如图所示：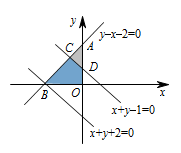
$ \Omega_1 $ 的区域如图中的三角形 $ ABO $ 所示，在 $ {\Omega _1} $ 中随机取一点，该点恰好在 $ \Omega_2 $ 的区域内的情况如图中的四边形 $ BCDO $ 所示，故所求概率为 $ \dfrac 78 $．
$ \Omega_1 $ 的区域如图中的三角形 $ ABO $ 所示，在 $ {\Omega _1} $ 中随机取一点，该点恰好在 $ \Omega_2 $ 的区域内的情况如图中的四边形 $ BCDO $ 所示，故所求概率为 $ \dfrac 78 $．
题目
答案
解析
备注
