查看数据源：599165c32bfec200011e0664
已知偶函数 $f\left( x \right)$ 在 $\left[ {0, + \infty } \right)$ 单调递减，$f\left( 2 \right) = 0$，若 $f\left( {x - 1} \right) > 0$，则 $x$ 的取值范围是 ．
【难度】
【出处】
2014年高考新课标Ⅱ卷（理）
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的奇偶性
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的单调性
  • 题型
    >
    函数
【答案】
$\left( - 1,3\right)$
【解析】
根据题中条件，可将 $f(x)$ 在 $(0,+\infty)$ 上的草图画出，再结合奇偶性，即可得到 $f(x)$ 的草图．然后结合图象求解不等式．因为 $f\left( x \right)$ 为偶函数，所以 $ f\left(x\right) $ 在 $ \left(-\infty,0\right] $ 单调递增，且 $ f\left(-2\right)=0 $．其示意图如图所示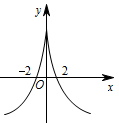：因为 $f\left( {x - 1} \right) > 0$，所以 $ -2<x - 1<2 $，解之得 $x\in\left( - 1,3\right)$．
题目 答案 解析 备注
0.116329s