如图，已知 $AB$，$BC$ 是 $ \odot O$ 的两条弦，$AO \perp BC$，$AB = \sqrt 3$，$BC = 2\sqrt 2 $，则 $ \odot O$ 的半径等于 ．
【难度】
【出处】
2014年高考湖南卷（理）
【标注】
【答案】
$\dfrac{3}{2}$
【解析】
本题考查相交弦定理，延长 $AO$ 得到相交弦是本题的关键．如图，设 $ AO$ 与 $ BC$ 交于点 $ D$，延长 $ AO $ 交圆于点 $ E $．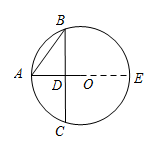
因为 $ AO\perp BC$，所以 $ D$ 为 $ BC$ 中点，因此，$BD=\dfrac12BC=\sqrt2$，$AD=\sqrt{AB^2-BD^2}=1$．由相交弦定理，得 $ BD\cdot DC=AD\cdot DE$，解得 $ DE=2$，所以 $AE=3$，故半径为 $\dfrac32$．
因为 $ AO\perp BC$，所以 $ D$ 为 $ BC$ 中点，因此，$BD=\dfrac12BC=\sqrt2$，$AD=\sqrt{AB^2-BD^2}=1$．由相交弦定理，得 $ BD\cdot DC=AD\cdot DE$，解得 $ DE=2$，所以 $AE=3$，故半径为 $\dfrac32$．
题目
答案
解析
备注
