直线 ${l_1}:y = x + a$ 和 ${l_2}:y = x + b$ 将单位圆 $C:{x^2} + {y^2} = 1$ 分成长度相等的四段弧，则 ${a^2} + {b^2} = $ ．
【难度】
【出处】
2014年高考湖北卷（理）
【标注】
【答案】
$ 2 $
【解析】
因为 ${l_1}:y = x + a$ 和 ${l_2}:y = x + b$ 将单位圆 $C:{x^2} + {y^2} = 1$ 分成长度相等的四段弧，所以每段弧所对的圆心角都为 $90^\circ$．圆 $C$ 为圆心在坐标原点的单位圆且 $l_1$ 和 $l_2$ 的斜率都为 $1$，所以 $l_1$ 和 $l_2$ 的位置如图所示．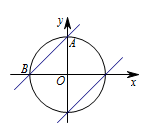
所以 $a=b=1$，于是 ${a^2} + {b^2} =2$．
所以 $a=b=1$，于是 ${a^2} + {b^2} =2$．
题目
答案
解析
备注
