三棱锥 $P - ABC$ 中，$D$，$E$ 分别为 $PB$，$PC$ 的中点，记三棱锥 $D - ABE$ 的体积为 ${V_1}$，$P - ABC$ 的体积为 ${V_2}$，则 $\dfrac{V_1}{V_2} = $ ．
【难度】
【出处】
2014年高考山东卷（理）
【标注】
【答案】
$ \dfrac 1 4 $
【解析】
此题考查了空间几何体的体积，此题是求比值关系，关键是能够转换顶点，以便能够求出底面面积的比值与高的比值．三棱锥 $P-ABC$ 如图所示：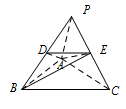
设 $C$ 到面 $ABP$ 的距离为 $h_1$，$E$ 到面 $ABP$ 的距离为 $h_2$，因为 $E$ 为 $CP$ 的中点，所以 $h_1=2h_2$．$D$ 为 $PB$ 的中点，所以 $S_{\triangle ABP}=2S_{\triangle ABD}$．故 $\dfrac{V_1}{V_2}=\dfrac{V_{E-ABD}}{V_{C-ABP}}=\dfrac{\dfrac{1}{3}\times S_{\triangle ABD}\times h_2}{\dfrac{1}{3}\times S_{\triangle ABP}\times h_1}=\dfrac{1}{4}$．
设 $C$ 到面 $ABP$ 的距离为 $h_1$，$E$ 到面 $ABP$ 的距离为 $h_2$，因为 $E$ 为 $CP$ 的中点，所以 $h_1=2h_2$．$D$ 为 $PB$ 的中点，所以 $S_{\triangle ABP}=2S_{\triangle ABD}$．故 $\dfrac{V_1}{V_2}=\dfrac{V_{E-ABD}}{V_{C-ABP}}=\dfrac{\dfrac{1}{3}\times S_{\triangle ABD}\times h_2}{\dfrac{1}{3}\times S_{\triangle ABP}\times h_1}=\dfrac{1}{4}$．
题目
答案
解析
备注
