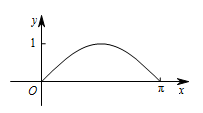
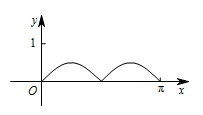
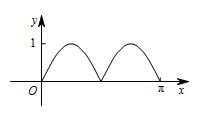
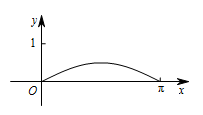
如图,圆 $O$ 的半径为 $ 1 $,$A$ 是圆上的定点,$P$ 是圆上的动点,角 $x$ 的始边为射线 $OA$,终边为射线 $OP$,过点 $P$ 作直线 $OA$ 的垂线,垂足为 $M$,将点 $M$ 到直线 $OP$ 的距离表示为 $x$ 的函数 $f\left(x\right)$,则 $y = f\left(x\right)$ 在 $\left[ {0,{\mathrm \pi} } \right]$ 上的图象大致为 \((\qquad)\) 

【难度】
【出处】
2014年高考新课标Ⅰ卷(理)
【标注】
【答案】
B
【解析】
本题考查三角函数的概念,利用已知关系表示函数 $f\left(x\right)$ 的解析式,分析其图象性质.当 $x=0,\dfrac {\mathrm \pi} {2},{\mathrm \pi} $ 时,$f\left(x\right)=0$;
当 $0<x<\dfrac{\mathrm \pi} {2}$ 时,$OM=\cos x $,$ f\left(x\right)=OM\cdot \sin x=\cos x\cdot \sin x=\dfrac 12\sin{2x} $;
当 $\dfrac{\mathrm \pi} {2}<x<{\mathrm \pi} $ 时,$OM=\cos \left({\mathrm \pi} -x\right) $,$f\left(x\right)=OM\cdot \sin\left({\mathrm \pi} -x\right)=\cos \left({\mathrm \pi} -x\right)\cdot \sin\left({\mathrm \pi} -x\right)=-\dfrac 12 \sin {2x}$.结合选项可得答案.
当 $0<x<\dfrac{\mathrm \pi} {2}$ 时,$OM=\cos x $,$ f\left(x\right)=OM\cdot \sin x=\cos x\cdot \sin x=\dfrac 12\sin{2x} $;
当 $\dfrac{\mathrm \pi} {2}<x<{\mathrm \pi} $ 时,$OM=\cos \left({\mathrm \pi} -x\right) $,$f\left(x\right)=OM\cdot \sin\left({\mathrm \pi} -x\right)=\cos \left({\mathrm \pi} -x\right)\cdot \sin\left({\mathrm \pi} -x\right)=-\dfrac 12 \sin {2x}$.结合选项可得答案.
题目
答案
解析
备注