设 $\overrightarrow {e_1} $，$\overrightarrow {e_2} $ 为单位向量，非零向量 $\overrightarrow b = x\overrightarrow {e_1} + y\overrightarrow {e_2}$，$x,y \in {\mathbb{R}}$，若 $\overrightarrow {e_1} ,\overrightarrow {e_2} $ 的夹角为 $\dfrac{\mathrm \pi} {6}$，则 $\dfrac{| x |}{{ \left| {\overrightarrow b } \right |}}$ 的最大值等于 ．
【难度】
【出处】
2013年高考浙江卷（文）
【标注】
【答案】
$ 2 $
【解析】
本题需要充分考虑向量分解的几何意义，借助正弦定理、二次函数等内容来求解．如图，记 $\overrightarrow{OA}=x\overrightarrow{e_1}$，$\overrightarrow{OB}=y\overrightarrow{e_2}$，则 $\overrightarrow{OC}=\overrightarrow{b}$，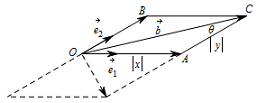
在 $\triangle OAC$ 中，由正弦定理得\[\dfrac{| x |}{{ \left| {\overrightarrow b } \right |}}=\dfrac{\sin\theta}{\sin \dfrac{\mathrm \pi} {6}}=2\sin\theta,\]其中 $\theta=\angle OCA$．
所以 $\dfrac{| x |}{{ \left| {\overrightarrow b } \right |}}\leqslant 2$，且等号可取到，如图中虚线所示，此时 $\dfrac xy=-\dfrac{2}{\sqrt 3}$．
其他方法：
为了便于计算可先求 ${\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2}$ 的范围，再求 $\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}$ 的最值．
根据题意，得\[\begin{split} {\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2} &= \dfrac{x^2}{{{{\left( {x\overrightarrow {e_1} + y\overrightarrow {e_2} } \right)}^2}}} \\ & = \dfrac{x^2}{{{{\left( {x\overrightarrow {e_1} } \right)}^2} + {{\left( {y\overrightarrow {e_2} } \right)}^2} + 2xy\overrightarrow {e_1} \cdot \overrightarrow {e_2} }} \\ & = \dfrac{1}{{1 + {{\left( {\dfrac{y}{x}} \right)}^2} + \dfrac{\sqrt 3 y}{x}}} \\ & = \dfrac{1}{{{{\left( {\dfrac{y}{x} + \dfrac{\sqrt 3 }{2}} \right)}^2} + \dfrac{1}{4}}}.\end{split} \]（推导中用到：）因为 ${\left( {\dfrac{y}{x} + \dfrac{\sqrt 3 }{2}} \right)^2} + \dfrac{1}{4} \geqslant \dfrac{1}{4}$，所以 $0 < {\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2} \leqslant 4$，所以\[0 < \dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}} \leqslant 2.\]故 $\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}$ 的最大值为 $ 2 $．
在 $\triangle OAC$ 中，由正弦定理得\[\dfrac{| x |}{{ \left| {\overrightarrow b } \right |}}=\dfrac{\sin\theta}{\sin \dfrac{\mathrm \pi} {6}}=2\sin\theta,\]其中 $\theta=\angle OCA$．所以 $\dfrac{| x |}{{ \left| {\overrightarrow b } \right |}}\leqslant 2$，且等号可取到，如图中虚线所示，此时 $\dfrac xy=-\dfrac{2}{\sqrt 3}$．
其他方法：
为了便于计算可先求 ${\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2}$ 的范围，再求 $\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}$ 的最值．
根据题意，得\[\begin{split} {\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2} &= \dfrac{x^2}{{{{\left( {x\overrightarrow {e_1} + y\overrightarrow {e_2} } \right)}^2}}} \\ & = \dfrac{x^2}{{{{\left( {x\overrightarrow {e_1} } \right)}^2} + {{\left( {y\overrightarrow {e_2} } \right)}^2} + 2xy\overrightarrow {e_1} \cdot \overrightarrow {e_2} }} \\ & = \dfrac{1}{{1 + {{\left( {\dfrac{y}{x}} \right)}^2} + \dfrac{\sqrt 3 y}{x}}} \\ & = \dfrac{1}{{{{\left( {\dfrac{y}{x} + \dfrac{\sqrt 3 }{2}} \right)}^2} + \dfrac{1}{4}}}.\end{split} \]（推导中用到：）因为 ${\left( {\dfrac{y}{x} + \dfrac{\sqrt 3 }{2}} \right)^2} + \dfrac{1}{4} \geqslant \dfrac{1}{4}$，所以 $0 < {\left( {\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}} \right)^2} \leqslant 4$，所以\[0 < \dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}} \leqslant 2.\]故 $\dfrac{\left| x \right|}{{\left| {\overrightarrow b } \right|}}$ 的最大值为 $ 2 $．
题目
答案
解析
备注
