不等式组 ${\begin{cases}
x + y \geqslant 1, \\
x - 2y \leqslant 4 \\
\end{cases}}$ 的解集记为 $ D $．有下面四个命题：
${p_1}:\forall \left(x,y\right) \in D,x + 2y \geqslant - 2$；${p_2}:\exists \left(x,y\right) \in D,x + 2y \geqslant 2$；
${p_3}:\forall \left(x,y\right) \in D,x + 2y \leqslant 3$；${p_4}:\exists \left(x,y\right) \in D,x + 2y \leqslant - 1$．
其中的真命题是 \((\qquad)\)
x + y \geqslant 1, \\
x - 2y \leqslant 4 \\
\end{cases}}$ 的解集记为 $ D $．有下面四个命题：
${p_1}:\forall \left(x,y\right) \in D,x + 2y \geqslant - 2$；${p_2}:\exists \left(x,y\right) \in D,x + 2y \geqslant 2$；
${p_3}:\forall \left(x,y\right) \in D,x + 2y \leqslant 3$；${p_4}:\exists \left(x,y\right) \in D,x + 2y \leqslant - 1$．
其中的真命题是 \((\qquad)\)
【难度】
【出处】
2014年高考新课标Ⅰ卷（理）
【标注】
【答案】
B
【解析】
本题考查线性规划相关知识．利用线性规划求目标函数的做法，分别判断出各个命题的正确性即可．不等式组表示的平面区域如图中阴影所示，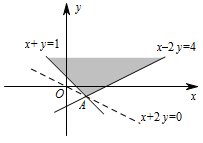
其中所有的点都满足 $x+2y\geqslant 0$，故 $p_1,p_2$ 为真．
其中所有的点都满足 $x+2y\geqslant 0$，故 $p_1,p_2$ 为真．
题目
答案
解析
备注
